بعد قليل بحول الله تعالى أقدم لكم
درس مختصر في التربوي - ضمن المعيار الرابع
(طرق التحليل الإحصائي)
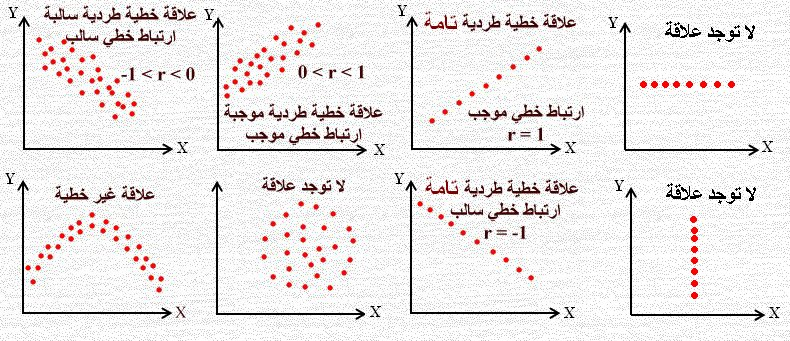
(أشكال الانتشار في الارتباط الخطي للمعاملات بين متغيرين)
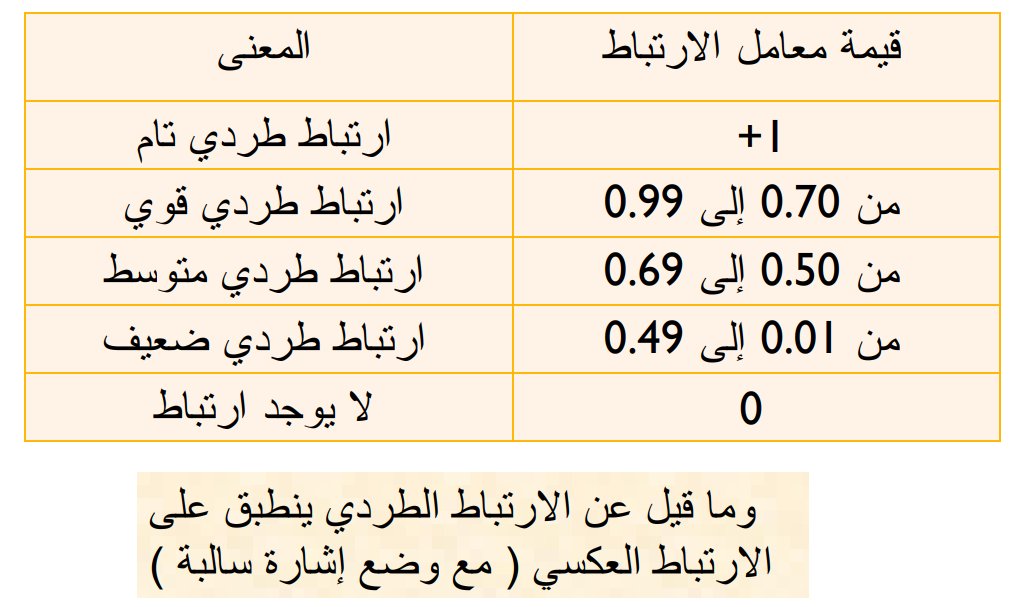
( جدول قيم معامل الارتباط )
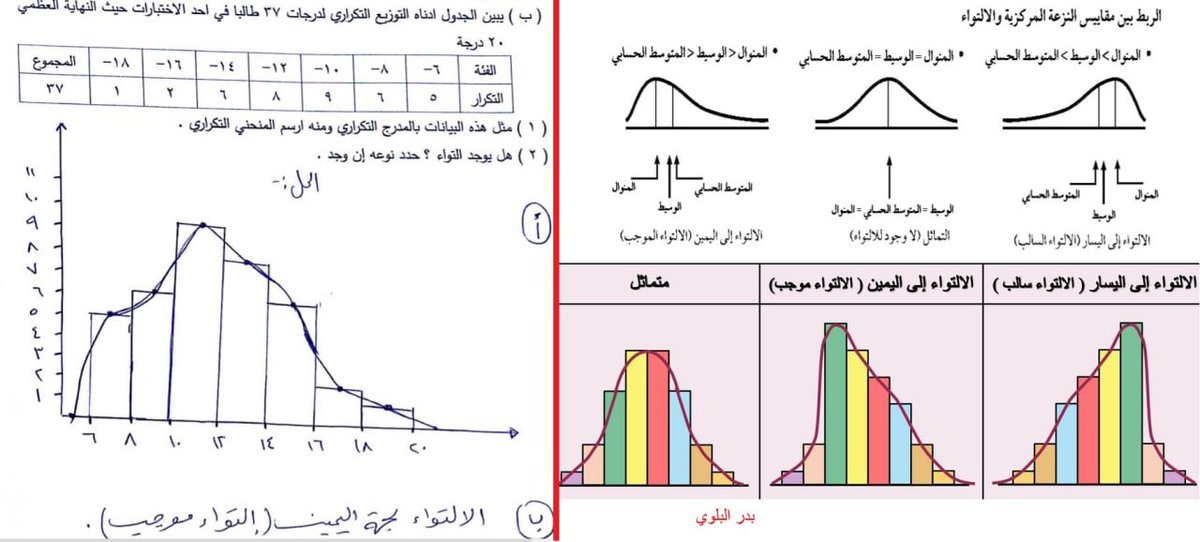
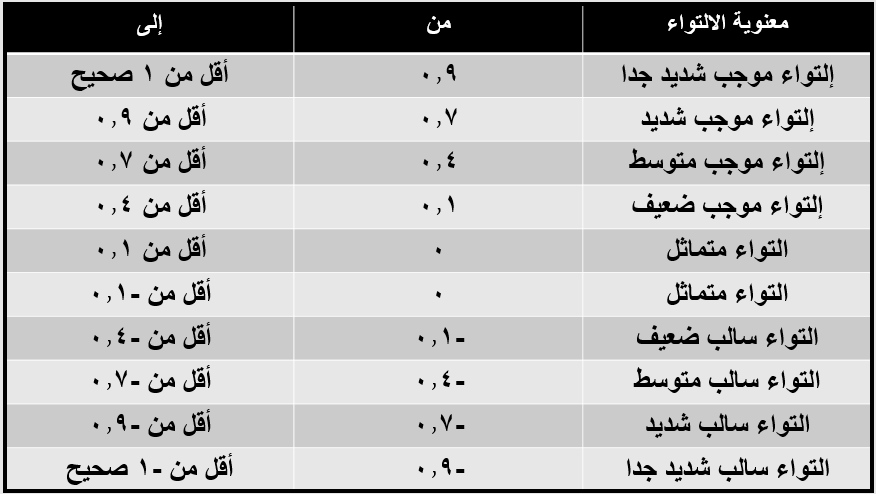
( الربط بين مقاييس النزعة المركزية والالتواء )
ضع هذه التغريدة في مفضلتك
درس مختصر في التربوي - ضمن المعيار الرابع
(طرق التحليل الإحصائي)
(أشكال الانتشار في الارتباط الخطي للمعاملات بين متغيرين)
( جدول قيم معامل الارتباط )
( الربط بين مقاييس النزعة المركزية والالتواء )
ضع هذه التغريدة في مفضلتك
1- من طرق التحليل الإحصائي
أ- مقاييس النزعة المركزية
للنزعة المركزية ثلاثة مقاييس وهي:
المتوسط الحسابي
والوسيط
والمنوال
أمثلة :
-المتوسط الحسابي = مجموع القيم ÷ عددها
مثال:
جد الوسط الحسابي للأعداد التالية: 3،2،4،6،10
= 25÷5= 5 وهو المتوسط الحسابي.
أ- مقاييس النزعة المركزية
للنزعة المركزية ثلاثة مقاييس وهي:
المتوسط الحسابي
والوسيط
والمنوال
أمثلة :
-المتوسط الحسابي = مجموع القيم ÷ عددها
مثال:
جد الوسط الحسابي للأعداد التالية: 3،2،4،6،10
= 25÷5= 5 وهو المتوسط الحسابي.
تابع أ- مقاييس النزعة المركزية
أمثلة
-المنوال: وهو الأكثر تكرارًا
تدريب:
جد المنوال لمجموعة الأعداد الآتية: 8,12,25,8,8,12,25,25,8
الحل: 8
أحياناً لا يكون هناك منوال فاختر إجابة : لا يوجد منوال
أمثلة
-المنوال: وهو الأكثر تكرارًا
تدريب:
جد المنوال لمجموعة الأعداد الآتية: 8,12,25,8,8,12,25,25,8
الحل: 8
أحياناً لا يكون هناك منوال فاختر إجابة : لا يوجد منوال
تابع أ- مقاييس النزعة المركزية
أمثلة
الوسيط
أ-ترتيب القيم تصاعديًا أو تنازليًا
ب- إن كان عدد القيم فرديًا فالوسيط هو ما يتوسط هذه القيم
مثال: 4،5،6،7،8 الوسيط هو 6
ج- إذا كان عدد القيم زوجيًا فالوسيط هو المتوسط الحسابي للعددين الأوسطين
انتهى شرح مقاييس النزعة المركزية
أمثلة
الوسيط
أ-ترتيب القيم تصاعديًا أو تنازليًا
ب- إن كان عدد القيم فرديًا فالوسيط هو ما يتوسط هذه القيم
مثال: 4،5،6،7،8 الوسيط هو 6
ج- إذا كان عدد القيم زوجيًا فالوسيط هو المتوسط الحسابي للعددين الأوسطين
انتهى شرح مقاييس النزعة المركزية
ب- مقاييس التشتت
لتحديد انحراف البيانات عن القيم الوسطية
وهي :
- المدى :وهو الفرق بين أكبر قيمة - أصغر قيمة
-الانحراف المعياري: وهو أكثر المقاييس استخدامًا ودقةً في حساب درجة التشتت.
-التباين: هو مقياس لانحراف القيم عن متوسطها الحسابي
لتحديد انحراف البيانات عن القيم الوسطية
وهي :
- المدى :وهو الفرق بين أكبر قيمة - أصغر قيمة
-الانحراف المعياري: وهو أكثر المقاييس استخدامًا ودقةً في حساب درجة التشتت.
-التباين: هو مقياس لانحراف القيم عن متوسطها الحسابي
تابع مقاييس التشتت
أمثلة
المدى: وقلنا هو الفرق بين أكبر قيمة - أصغر قيمة
مثال: أكبر درجة في مادة الرياضيات 10 وأصغر درجة 7
10 -7 = 3 وهو المدى
أمثلة
المدى: وقلنا هو الفرق بين أكبر قيمة - أصغر قيمة
مثال: أكبر درجة في مادة الرياضيات 10 وأصغر درجة 7
10 -7 = 3 وهو المدى
تابع مقاييس التشتت
أمثلة
الانحراف المعياري
أمثلة
الانحراف المعياري
تابع مقاييس التشتت
أمثلة
التباين
انتهى شرح مقاييس التشتت
أمثلة
التباين
انتهى شرح مقاييس التشتت
تدريبات
- إن طلب منك إيجاد قيمة التباين فاضرب العدد ( الانحراف المعياري ) في نفسه = الإجابة
5×5= 25
- إن طلب منك قيمة الانحراف المعياري ، فمن خيارات الإجابة ابحث عن العدد الذي إن ضربته في نفسه = قيمة الانحراف المعياري في العدد الموجود بالسؤال .
2×2= 4
- إن طلب منك إيجاد قيمة التباين فاضرب العدد ( الانحراف المعياري ) في نفسه = الإجابة
5×5= 25
- إن طلب منك قيمة الانحراف المعياري ، فمن خيارات الإجابة ابحث عن العدد الذي إن ضربته في نفسه = قيمة الانحراف المعياري في العدد الموجود بالسؤال .
2×2= 4
الدرجة المعيارية:
فائدتها : تحويل الدرجة الخام إلى درجة قابلة للمقارنة مع قيم أخرى
طريقة حسابها:
الدرجة الخام – الوسط الحسابي / الانحراف المعياري
تدريب ( صورة )
فائدتها : تحويل الدرجة الخام إلى درجة قابلة للمقارنة مع قيم أخرى
طريقة حسابها:
الدرجة الخام – الوسط الحسابي / الانحراف المعياري
تدريب ( صورة )
احفظ العبارات جيدًا . ( صور مهمة )
القيم المتطرفة : تعني القيم الغريبة بين القيم وقد تكون الأكبر أو الأصغر
تدريب: أوجد القيمة المتطرّفة من القيم التالية:
9، 5، 7، 4 ،23، 2
القيمة المتطرّفة هنا هي 23 لأنها قيمة كبيرة جدًا عن باقي القيم .
تدريب: أوجد القيمة المتطرّفة من القيم التالية:
9، 5، 7، 4 ،23، 2
القيمة المتطرّفة هنا هي 23 لأنها قيمة كبيرة جدًا عن باقي القيم .
انتهينا من شرح (طرق التحليل الإحصائي)
نُكمل ما تبقى لاحقًا بإذن الله تعالى
وهي سهلة بحول الله تعالى
نُكمل ما تبقى لاحقًا بإذن الله تعالى
وهي سهلة بحول الله تعالى
نأتي الآن إلى شرح
(أشكال الانتشار في الارتباط الخطي للمعاملات بين متغيرين)
أولاً نتحدث بإيجاز عن معاملات الارتباط والانحدار
الارتباط : هو تعيين طبيعة وقوة العلاقة بين متغيرين من عدمها.
معامل الارتباط = هو مؤشر هذه العلاقة
والخطوة في تحديد العلاقة هي رسم شكل الانتشار
(أشكال الانتشار في الارتباط الخطي للمعاملات بين متغيرين)
أولاً نتحدث بإيجاز عن معاملات الارتباط والانحدار
الارتباط : هو تعيين طبيعة وقوة العلاقة بين متغيرين من عدمها.
معامل الارتباط = هو مؤشر هذه العلاقة
والخطوة في تحديد العلاقة هي رسم شكل الانتشار
أنواع الارتباط :
ارتباط طردي موجب
ارتباط طردي سالب ( عكسي )
إذن لدينا إما علاقة طردية أو علاقة عكسية بين المتغيرين .
ارتباط طردي موجب
ارتباط طردي سالب ( عكسي )
إذن لدينا إما علاقة طردية أو علاقة عكسية بين المتغيرين .
توضيح مع الأمثلة
العلاقة الطردية :هي زيادة متغيرين أو نقصانهما مع بعض
مثال : التفوّق الدراسي / المذاكرة
كلما زادت المذاكرة زاد التفوّق الدراسي = علاقة طردية موجبة
العلاقة العكسية :متغيّر يزيد على حساب متغير ينقص
مثال : الإهمال الدراسي-التفوّق الدراسي
واحد يزيد والآخر ينقص
العلاقة الطردية :هي زيادة متغيرين أو نقصانهما مع بعض
مثال : التفوّق الدراسي / المذاكرة
كلما زادت المذاكرة زاد التفوّق الدراسي = علاقة طردية موجبة
العلاقة العكسية :متغيّر يزيد على حساب متغير ينقص
مثال : الإهمال الدراسي-التفوّق الدراسي
واحد يزيد والآخر ينقص
الآن نوضح هنا أشكال الانتشار في الارتباط الخطي للمعاملات بين متغيرين ، وعليك حفظها جيدًا :
هنا جدول ( جدول قيم معامل الارتباط ) يجب حفظه فقد ورد عليه سؤال في العام الماضي .
قياس الارتباط :
قياس الارتباط :
1-معامل بيرسون
من أكثر معاملات الارتباط استخداماً خاصة في العلوم الإنسانية و الاجتماعية .
كلا المتغيرين فيه مقياس فترة أو نسبي = بيانات كميّة
2-معامل سيبرمان
ارتباط متغيرين كلاً منهما من بيانات النوع ((الرتبي ))
من أكثر معاملات الارتباط استخداماً خاصة في العلوم الإنسانية و الاجتماعية .
كلا المتغيرين فيه مقياس فترة أو نسبي = بيانات كميّة
2-معامل سيبرمان
ارتباط متغيرين كلاً منهما من بيانات النوع ((الرتبي ))
3-معامل ارتباط فاي
ارتباط بين متغيرين اسميين كلاً منهما ثنائي التقسيم
مثل النوع : ذكر أو أنثى . المرض : مريض أو غير مريض
4-معامل بوينت بايسيريال
يستخدم لقياس علاقة الارتباط بين متغير كمي ومتغير اسمي
ذي مستويين كالإجابة بـ نعم أو لا أو الجنس : ذكر أو أنثى .
ارتباط بين متغيرين اسميين كلاً منهما ثنائي التقسيم
مثل النوع : ذكر أو أنثى . المرض : مريض أو غير مريض
4-معامل بوينت بايسيريال
يستخدم لقياس علاقة الارتباط بين متغير كمي ومتغير اسمي
ذي مستويين كالإجابة بـ نعم أو لا أو الجنس : ذكر أو أنثى .
أخيرًا في درس اليوم
( الربط بين مقاييس النزعة المركزية والالتواء )
التوزيع التكراري :
أ- التماثل
ب- الالتواء الموجب
ج- الالتواء السالب
( الربط بين مقاييس النزعة المركزية والالتواء )
التوزيع التكراري :
أ- التماثل
ب- الالتواء الموجب
ج- الالتواء السالب
درجات التواء البيانات في توزيعها حول المتوسط الحسابي لها تأخذ قيمة بين (+1) و (-1) بحيث تتفاوت درجاتها كما يوضحها الجدول التالي:
أضفها لمعلوماتك .
انتهينا بتوفيق الله من شرح بعض المواضيع عن التحليل الإحصائي لا تنسونا من الدعاء .
أضفها لمعلوماتك .
انتهينا بتوفيق الله من شرح بعض المواضيع عن التحليل الإحصائي لا تنسونا من الدعاء .
معلومة مهمة
ومن الممكن الاعتماد علـى البرمجيات الإحصائية التي تمكن مـن حساب معامل الارتباط بسهولة جدا، فمثال يمكن استخدام برنامـج SPSS لحساب معامل الارتباط بين متغيرين.
ومن الممكن الاعتماد علـى البرمجيات الإحصائية التي تمكن مـن حساب معامل الارتباط بسهولة جدا، فمثال يمكن استخدام برنامـج SPSS لحساب معامل الارتباط بين متغيرين.
جاري تحميل الاقتراحات...