1/N
This is a thread on Chhanda Shastra (छन्द शास्त्र), study of prosody, where ancient Indians invented groundbreaking mathematical concepts including binary representation, combinatorics, Pascal’s Triangle, & Fibonacci sequence at least 2000 years before they emerged in Europe x.com
This is a thread on Chhanda Shastra (छन्द शास्त्र), study of prosody, where ancient Indians invented groundbreaking mathematical concepts including binary representation, combinatorics, Pascal’s Triangle, & Fibonacci sequence at least 2000 years before they emerged in Europe x.com
2/N
I dedicate this thread to Saraswati - the divine architect of precision and grace. Tireless and unerring, she weaves order from chaos, forging beauty, harmony, and truth in every detail. x.com
I dedicate this thread to Saraswati - the divine architect of precision and grace. Tireless and unerring, she weaves order from chaos, forging beauty, harmony, and truth in every detail. x.com
3/N
In the vast array of knowledge systems invented in ancient India, Chhanda (छन्द) - the study of prosody - stands as a profound confluence of art, mathematics, and computational ingenuity.
In the vast array of knowledge systems invented in ancient India, Chhanda (छन्द) - the study of prosody - stands as a profound confluence of art, mathematics, and computational ingenuity.
4/N
At its core, Chhanda governs the rhythmic and melodic structures of Sanskrit poetry. It transforms language into an artistic expression, ensuring the perfect blend of syllables, sounds, and emotions.
At its core, Chhanda governs the rhythmic and melodic structures of Sanskrit poetry. It transforms language into an artistic expression, ensuring the perfect blend of syllables, sounds, and emotions.
5/N
The aesthetic appeal of Sanskrit poetry, from the lyrical Rigveda hymns to classical Sanskrit epics like Mahabharata and Ramayana, owes much to its well-defined metrical patterns as defined in the Chhanda Shastra .
The aesthetic appeal of Sanskrit poetry, from the lyrical Rigveda hymns to classical Sanskrit epics like Mahabharata and Ramayana, owes much to its well-defined metrical patterns as defined in the Chhanda Shastra .
6/N
Yet, Chhanda (छन्द) is far more than a poetic tool. The brilliance of Chhanda lies in how ancient Indian thinkers seamlessly wove together the seemingly disparate realms of music, linguistics, and computational recipes into a unified framework.
Yet, Chhanda (छन्द) is far more than a poetic tool. The brilliance of Chhanda lies in how ancient Indian thinkers seamlessly wove together the seemingly disparate realms of music, linguistics, and computational recipes into a unified framework.
7/N
Ancient Hindus and Jains, through Chhanda Shastra, laid the foundation for concepts like binary representation, combinatorics, recursion, iteration, and error correction - developing them more than 2,500 years ago, nearly two millennia before these ideas appeared in Europe.
Ancient Hindus and Jains, through Chhanda Shastra, laid the foundation for concepts like binary representation, combinatorics, recursion, iteration, and error correction - developing them more than 2,500 years ago, nearly two millennia before these ideas appeared in Europe.
8/N
This is a comprehensive thread, so I’ve organized it into multiple sections for better readability. x.com
This is a comprehensive thread, so I’ve organized it into multiple sections for better readability. x.com
9/N
The history of Chhanda (छन्द), the science of prosody, is a fascinating journey that weaves together poetry, linguistics, music, mathematics, and philosophy, forming a cornerstone of ancient Indian intellectual traditions. x.com
The history of Chhanda (छन्द), the science of prosody, is a fascinating journey that weaves together poetry, linguistics, music, mathematics, and philosophy, forming a cornerstone of ancient Indian intellectual traditions. x.com
10/N
Chhanda finds its earliest mention in the Vedas, where it was revered as one of the six Vedāṅgas (limbs of the Vedas), essential for correct recitation. Its precise meters ensured the phonetic purity of these sacred texts.
Chhanda finds its earliest mention in the Vedas, where it was revered as one of the six Vedāṅgas (limbs of the Vedas), essential for correct recitation. Its precise meters ensured the phonetic purity of these sacred texts.
11/N
The Purusha Sukta of the Rig Veda declares Chhanda as born from the cosmic Purusha’s Yajña - elevating it to the divine rhythm of manifestation, the pulse of universal harmony, and the very essence of eternal truth. x.com
The Purusha Sukta of the Rig Veda declares Chhanda as born from the cosmic Purusha’s Yajña - elevating it to the divine rhythm of manifestation, the pulse of universal harmony, and the very essence of eternal truth. x.com
12/N
Purusha is the eternal, unchanging consciousness. It is the whole of existence - macrocosm (universe) and microcosm (individual being).
Purusha is the eternal, unchanging consciousness. It is the whole of existence - macrocosm (universe) and microcosm (individual being).
13/N
Yajña symbolizes Purusha's self-offering where all of existence emerges as a divine manifestation. It is the metaphysical truth of the One becoming the many, eternally sustaining and evolving life.
Yajña symbolizes Purusha's self-offering where all of existence emerges as a divine manifestation. It is the metaphysical truth of the One becoming the many, eternally sustaining and evolving life.
14/N
The Ṛks are the first vibration of truth, the primal expressions of the cosmic spirit in sound and word, embodying the essence of divine thought.
The Ṛks are the first vibration of truth, the primal expressions of the cosmic spirit in sound and word, embodying the essence of divine thought.
15/N
The Sāma chants are the melodies of the infinite, representing the soul’s longing to harmonize with the divine, the music that binds creation in the rhythm of bliss.
The Sāma chants are the melodies of the infinite, representing the soul’s longing to harmonize with the divine, the music that binds creation in the rhythm of bliss.
16/N
The Yajus signify the divine action, the will of the Purusha shaping the cosmos, guiding the forces of creation toward harmony and purpose.
The Yajus signify the divine action, the will of the Purusha shaping the cosmos, guiding the forces of creation toward harmony and purpose.
17/N
The Chhandas are the hidden structures of the universe, the eternal rhythms that govern all creation, akin to the pulse of time and the heartbeat of cosmic order (Rita).
The Chhandas are the hidden structures of the universe, the eternal rhythms that govern all creation, akin to the pulse of time and the heartbeat of cosmic order (Rita).
19/N
Systematic study of the science of prosody (Chhanda) has a very long history and legacy in ancient india spanning over at least 2500 years
Systematic study of the science of prosody (Chhanda) has a very long history and legacy in ancient india spanning over at least 2500 years
20/N
The table below lists some of the important ancient Indian texts on prosody, many of which include discussions of computational algorithms or recipes designed for enumerating, lookup or combinatorial visualization in the field of prosody. x.com
The table below lists some of the important ancient Indian texts on prosody, many of which include discussions of computational algorithms or recipes designed for enumerating, lookup or combinatorial visualization in the field of prosody. x.com
21/N
The earliest surviving and most important work in Sanskrit prosody is Chandaḥ Sūtraṁ, a magnum opus of sage Piṅgala Nāga, popularly called Ācārya Piṅgala or simply Piṅgala
The earliest surviving and most important work in Sanskrit prosody is Chandaḥ Sūtraṁ, a magnum opus of sage Piṅgala Nāga, popularly called Ācārya Piṅgala or simply Piṅgala
22/N
The Chhandaśāstra of Piṅgala (~300 BCE) marked a turning point, transforming Chhanda into a computational science. Pingala introduced algorithms to enumerate, analyze, and classify meters, making Chhanda a bridge between art and mathematics.
The Chhandaśāstra of Piṅgala (~300 BCE) marked a turning point, transforming Chhanda into a computational science. Pingala introduced algorithms to enumerate, analyze, and classify meters, making Chhanda a bridge between art and mathematics.
23/N
While Piṅgala’s Chhandaśāstra is one of the significant contributions to Sanskrit prosody, it does not exist in isolation. It is founded upon the remarkable legacy of advanced scientific exploration of prosody that ancient India cultivated over thousands of years
While Piṅgala’s Chhandaśāstra is one of the significant contributions to Sanskrit prosody, it does not exist in isolation. It is founded upon the remarkable legacy of advanced scientific exploration of prosody that ancient India cultivated over thousands of years
24/N
Piṅgala has referred the work of some of his predecessors by name. They are: Kāśyapa (7.9, i.e. 9th sūtra of 7th chapter). Krausṭuki (3.29), Tāṇḍi (3.36), Yāska (3.30), Rāta-Māṇḍavya (7.35), Śākalya (7.9) and Saitava (5.8, 7.10)
Piṅgala has referred the work of some of his predecessors by name. They are: Kāśyapa (7.9, i.e. 9th sūtra of 7th chapter). Krausṭuki (3.29), Tāṇḍi (3.36), Yāska (3.30), Rāta-Māṇḍavya (7.35), Śākalya (7.9) and Saitava (5.8, 7.10)
25/N
Pingala's contributions to the theory of Chhanda are profound and multifaceted, forming a foundational framework for combinatorics, binary representation, and algorithmic processes. His key contributions include the following (....thread continues) x.com
Pingala's contributions to the theory of Chhanda are profound and multifaceted, forming a foundational framework for combinatorics, binary representation, and algorithmic processes. His key contributions include the following (....thread continues) x.com
26/N
These contributions not only advanced the study of Sanskrit prosody but also influenced the development of mathematical and computational ideas, cementing Pingala’s legacy as a visionary thinker in both literature and science.
These contributions not only advanced the study of Sanskrit prosody but also influenced the development of mathematical and computational ideas, cementing Pingala’s legacy as a visionary thinker in both literature and science.
27/N
With the rise of Sanskrit literature, Chhanda, which had deep roots in both Vedic rituals & artistic expression, evolved into a creative tool for poets like Kālidāsa, who employed intricate meters such as Mandākrānta & Śārdūlavikrīḍita to infuse lyrical beauty into works.
With the rise of Sanskrit literature, Chhanda, which had deep roots in both Vedic rituals & artistic expression, evolved into a creative tool for poets like Kālidāsa, who employed intricate meters such as Mandākrānta & Śārdūlavikrīḍita to infuse lyrical beauty into works.
28/N
Post-Pingala, Chhanda flourished in classical Sanskrit poetry, where it became a defining feature of aesthetic expression. Poets meticulously crafted verses using a vast array of meters, each evoking a unique emotional resonance.
Post-Pingala, Chhanda flourished in classical Sanskrit poetry, where it became a defining feature of aesthetic expression. Poets meticulously crafted verses using a vast array of meters, each evoking a unique emotional resonance.
29/N
In Indian classical music, Chhanda influenced the development of tālas (rhythmic cycles), with short and long beats mirroring laghu and guru syllables. It became the foundation of rhythmic improvisation and composition.
In Indian classical music, Chhanda influenced the development of tālas (rhythmic cycles), with short and long beats mirroring laghu and guru syllables. It became the foundation of rhythmic improvisation and composition.
30/N
The interplay of short and long syllables in Chhanda also shaped Indian classical dance, where choreographers used metrical patterns to design intricate footwork sequences, blending precision with artistry.
The interplay of short and long syllables in Chhanda also shaped Indian classical dance, where choreographers used metrical patterns to design intricate footwork sequences, blending precision with artistry.
31/N
Chhanda’s integration of music, mathematics, and linguistics inspired interdisciplinary scholarship.
Chhanda’s integration of music, mathematics, and linguistics inspired interdisciplinary scholarship.
32/N
In medieval India, Chhanda was further studied and systematized by scholars like Halāyudha, whose commentaries on Pingala expanded its mathematical and linguistic scope.
In medieval India, Chhanda was further studied and systematized by scholars like Halāyudha, whose commentaries on Pingala expanded its mathematical and linguistic scope.
33/N
Despite its ancient origins, Chhanda’s relevance persists. Modern fields like natural language processing, algorithm design, and music theory draw parallels to its methods, showing its timeless ingenuity.
Despite its ancient origins, Chhanda’s relevance persists. Modern fields like natural language processing, algorithm design, and music theory draw parallels to its methods, showing its timeless ingenuity.
34/N
The history of Chhanda is a testament to ancient India’s holistic approach to knowledge, where art, science, and spirituality converged. It reveals a tradition that valued both precision and creativity, leaving a legacy that continues to inspire.
The history of Chhanda is a testament to ancient India’s holistic approach to knowledge, where art, science, and spirituality converged. It reveals a tradition that valued both precision and creativity, leaving a legacy that continues to inspire.
36/N
The importance of “Chhanda” (छन्द / Prosody) has been very elegantly explained in Nāṭya Shāstra (नाट्य शास्त्र), a grand Sanskrit treatise on the performing arts. The text has been composed by sage Bharata no later than 200 BCE. x.com
The importance of “Chhanda” (छन्द / Prosody) has been very elegantly explained in Nāṭya Shāstra (नाट्य शास्त्र), a grand Sanskrit treatise on the performing arts. The text has been composed by sage Bharata no later than 200 BCE. x.com
37/N
This verse beautifully encapsulates the symbiotic relationship between meter (छन्द) and sound (शब्द), emphasizing their indispensable role in the art of natya (performing arts).
This verse beautifully encapsulates the symbiotic relationship between meter (छन्द) and sound (शब्द), emphasizing their indispensable role in the art of natya (performing arts).
38/N
Just as sound gains structure through meter, meter is meaningless without the element of sound. In natya, the synchronization of linguistic expression with rhythmic patterns enhances the beauty & effectiveness of the performance
Just as sound gains structure through meter, meter is meaningless without the element of sound. In natya, the synchronization of linguistic expression with rhythmic patterns enhances the beauty & effectiveness of the performance
39/N
Nāṭya Shāstra tells us that Chhanda (छन्द) or Meter is an integral part of expression in any knowledge framework invented & systematized in ancient India.
Nāṭya Shāstra tells us that Chhanda (छन्द) or Meter is an integral part of expression in any knowledge framework invented & systematized in ancient India.
40/N
But what is the definition of Chhanda (छन्द) ? We get a very terse and useful definition of Chhanda in Ṛk Sarvānukramaṇī (ऋक् सर्वानुक्रमणी) composed by Kātyāyana no later than 600 BCE
But what is the definition of Chhanda (छन्द) ? We get a very terse and useful definition of Chhanda in Ṛk Sarvānukramaṇī (ऋक् सर्वानुक्रमणी) composed by Kātyāyana no later than 600 BCE
41/N
The Ṛk Sarvānukramaṇī of Kātyāyana is an ancient Sanskrit text that serves as an index and catalog of the Ṛgveda. It is one of the oldest and most important anukramaṇīs (indices or glossaries) associated with Vedic literature.
The Ṛk Sarvānukramaṇī of Kātyāyana is an ancient Sanskrit text that serves as an index and catalog of the Ṛgveda. It is one of the oldest and most important anukramaṇīs (indices or glossaries) associated with Vedic literature.
42/N
The text systematically lists the contents of the Ṛgveda in terms of its ṛṣis (seers), devatās (deities), and chhandas (meters) for each hymn and verse.
The text systematically lists the contents of the Ṛgveda in terms of its ṛṣis (seers), devatās (deities), and chhandas (meters) for each hymn and verse.
43/N
Here is the definition of Chhanda (छन्द) from Ṛk Sarvānukramaṇī of Kātyāyana - “That which is measured by syllables (अक्षर) is Chhanda (छन्द)” x.com
Here is the definition of Chhanda (छन्द) from Ṛk Sarvānukramaṇī of Kātyāyana - “That which is measured by syllables (अक्षर) is Chhanda (छन्द)” x.com
44/N
This definition of Chhanda emphasizes that the structure of meter is determined by the the arrangement, count and emphasis of syllables or अक्षर
This definition of Chhanda emphasizes that the structure of meter is determined by the the arrangement, count and emphasis of syllables or अक्षर
45/N
The purpose of this section is to make you familiar with some of the core concepts of Chhanda Shastra (field of Prosody) as systematized by ancient Indian scientists such as Pingala, Bharata, Brahmagupta, Kedarabhatta, etc. x.com
The purpose of this section is to make you familiar with some of the core concepts of Chhanda Shastra (field of Prosody) as systematized by ancient Indian scientists such as Pingala, Bharata, Brahmagupta, Kedarabhatta, etc. x.com
46/N
Below you see an architecture diagram of Chhanda, which shows major concepts of Chhanda Shastra and how they are related x.com
Below you see an architecture diagram of Chhanda, which shows major concepts of Chhanda Shastra and how they are related x.com
47/N
A complete analysis of all the concepts of Chhanda is beyond the scope of this thread. But we are going to review the ones that are relevant for computational analysis.
A complete analysis of all the concepts of Chhanda is beyond the scope of this thread. But we are going to review the ones that are relevant for computational analysis.
48/N
We are going to review the concepts in the architecture of Chhanda, analyze their relevance in the big picture and will get familiar with the essence of theory or Prosody as viewed by the ancient Indian (Hindu / Jain) musicians, mathematicians and computational linguists.
We are going to review the concepts in the architecture of Chhanda, analyze their relevance in the big picture and will get familiar with the essence of theory or Prosody as viewed by the ancient Indian (Hindu / Jain) musicians, mathematicians and computational linguists.
49/N
In Sanskrit, literary compositions (काव्य / kāvya) are created in two forms: prose (गद्य gadya) and verse (पद्य / padya). A padya refers to a stanza or verse, which is generally composed of four pādas (पाद) or metrical lines.
In Sanskrit, literary compositions (काव्य / kāvya) are created in two forms: prose (गद्य gadya) and verse (पद्य / padya). A padya refers to a stanza or verse, which is generally composed of four pādas (पाद) or metrical lines.
50/N
Sanskrit verses are typically composed of four lines, each called a pāda (पाद) or quarter. The first two pādas form the first half of the verse, and the last two pādas form the second half.
(the thread continues...)
Sanskrit verses are typically composed of four lines, each called a pāda (पाद) or quarter. The first two pādas form the first half of the verse, and the last two pādas form the second half.
(the thread continues...)
51/N
Chhanda (छन्द) is the systematic arrangement of syllables in Sanskrit poetry, categorized by the number and pattern of short and long syllables in each quarter (pāda) of a verse. It forms the metrical structure of Sanskrit literature.
Chhanda (छन्द) is the systematic arrangement of syllables in Sanskrit poetry, categorized by the number and pattern of short and long syllables in each quarter (pāda) of a verse. It forms the metrical structure of Sanskrit literature.
52/N
A pāda is structured based on either the number of syllables ( अक्षर / Akshara ) or the number of syllabic instants (मात्रा / mātrā), which denote the duration of syllables.
A pāda is structured based on either the number of syllables ( अक्षर / Akshara ) or the number of syllabic instants (मात्रा / mātrā), which denote the duration of syllables.
53/N
An Akshara (अक्षर) is a vowel or a vowel with one or more consonants preceding it. An Akshara is a unit of sound that can be pronounced clearly in a single vocal effort. It represents a syllable.
An Akshara (अक्षर) is a vowel or a vowel with one or more consonants preceding it. An Akshara is a unit of sound that can be pronounced clearly in a single vocal effort. It represents a syllable.
54/N
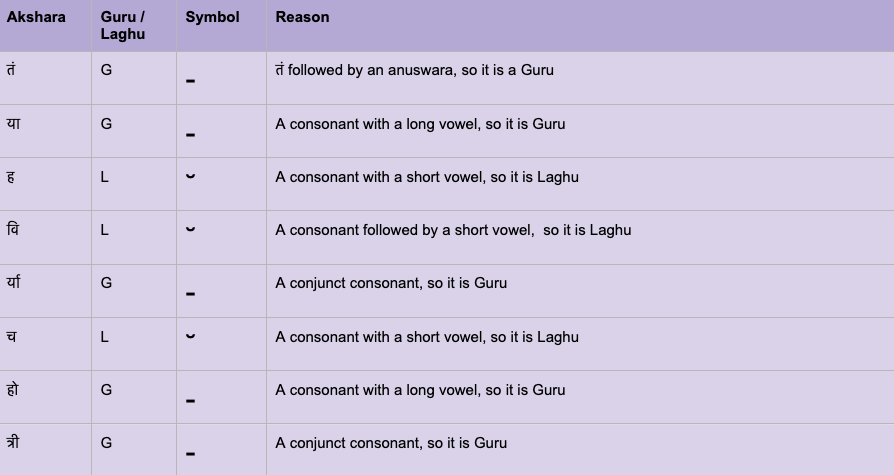
An Akshara (अक्षर) can be short (लघु / Laghu) or long (गुरु / Guru)
An Akshara (अक्षर) can be short (लघु / Laghu) or long (गुरु / Guru)
57/N
Sometimes a short or a laghu syllable will be considered as a long or guru syllable. The rules are given below: x.com
Sometimes a short or a laghu syllable will be considered as a long or guru syllable. The rules are given below: x.com
58/N
Sometimes (not very often) the metrical requirements dictate the classification of a syllable x.com
Sometimes (not very often) the metrical requirements dictate the classification of a syllable x.com
59/N
Let’s analyze the first verse of Kalidas’s Abhijnanashakuntalam in the light of Chhanda or theory of prosody. x.com
Let’s analyze the first verse of Kalidas’s Abhijnanashakuntalam in the light of Chhanda or theory of prosody. x.com
60/N
We will break down each syllable of the first line (pāda) of the first verse of Kalidas’s Abhijnanashakuntalam according to the syllable classification rules in Chhanda Shastra x.com
We will break down each syllable of the first line (pāda) of the first verse of Kalidas’s Abhijnanashakuntalam according to the syllable classification rules in Chhanda Shastra x.com
61/N
Continuing with the markup of each syllable of the first verse of Kalidas’s Abhijnanashakuntalam x.com
Continuing with the markup of each syllable of the first verse of Kalidas’s Abhijnanashakuntalam x.com
63/N
Another important concept in Sanskrit prosody is that of mātrā (मात्रा). A unit of metrical quantity is called a mātrā, or "instant." A mātrā represents the time required to pronounce a short vowel. x.com
Another important concept in Sanskrit prosody is that of mātrā (मात्रा). A unit of metrical quantity is called a mātrā, or "instant." A mātrā represents the time required to pronounce a short vowel. x.com
64/N
Chhanda is categorized broadly into two systems: Vṛtta (वृत्त or fixed syllabic patterns) and Jāti (जाति or mātrā-based patterns). The former is used in classical poetry; the latter dominates Vedic recitations.
Chhanda is categorized broadly into two systems: Vṛtta (वृत्त or fixed syllabic patterns) and Jāti (जाति or mātrā-based patterns). The former is used in classical poetry; the latter dominates Vedic recitations.
65/N
Vṛttattachanda (वृत्तत्छन्द) refers to a metrical structure regulated by the number and placement of syllables (laghu and guru) in each pāda (quarter) of a verse. The categories of Vṛttattachanda are given below x.com
Vṛttattachanda (वृत्तत्छन्द) refers to a metrical structure regulated by the number and placement of syllables (laghu and guru) in each pāda (quarter) of a verse. The categories of Vṛttattachanda are given below x.com
66/N
Samavṛtta (समवृत्त) refers to verses where all four pādas (quarters) have an equal number of syllables. Common examples include meters like Anuṣṭup (अनुष्टुप्) and Indravajrā (इन्द्रवज्रा). Details of this subcategory are given below x.com
Samavṛtta (समवृत्त) refers to verses where all four pādas (quarters) have an equal number of syllables. Common examples include meters like Anuṣṭup (अनुष्टुप्) and Indravajrā (इन्द्रवज्रा). Details of this subcategory are given below x.com
67/N
An example of a Samavṛtta verse in the Indravajrā meter is found in Kālidāsa's "Kumārasambhavam": x.com
An example of a Samavṛtta verse in the Indravajrā meter is found in Kālidāsa's "Kumārasambhavam": x.com
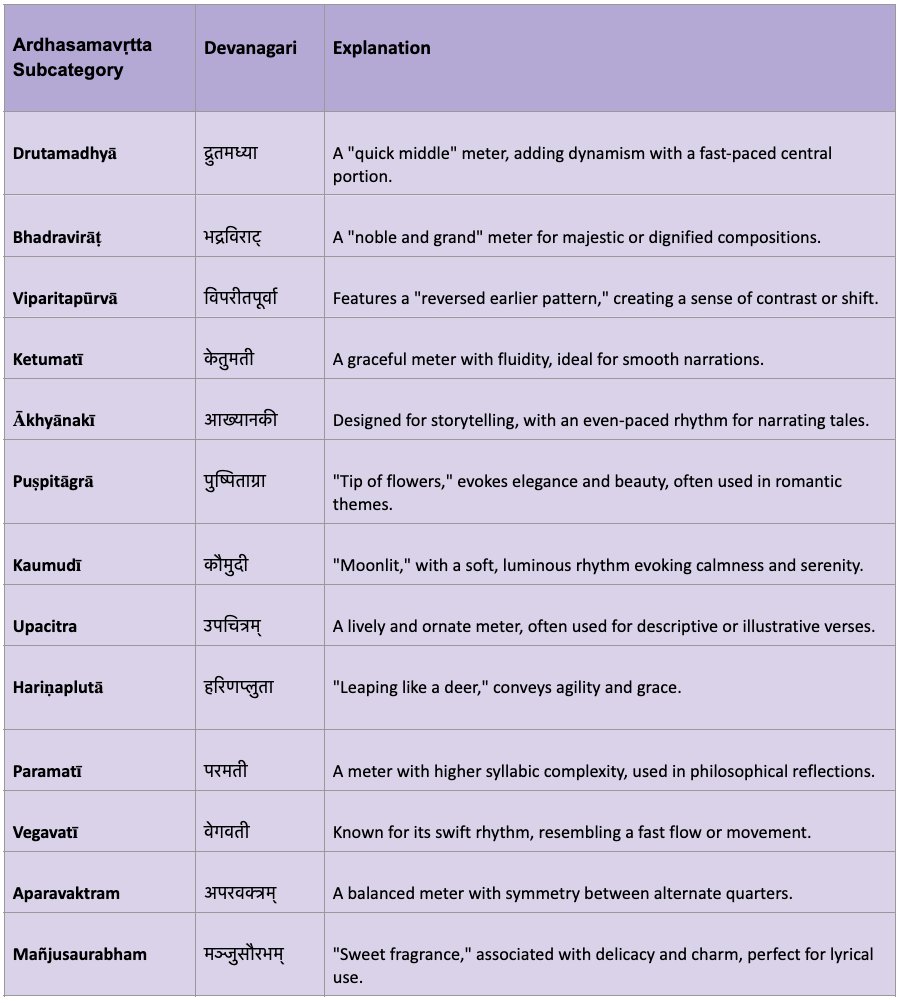
68/N
Ardhasamavṛtta (अर्धसमवृत्त) or Half-even meters refers to meters where alternate quarters of a verse have the same structure. For example: the 1st quarter is similar to the 3rd quarter, and the 2nd quarter is similar to the 4th quarter.
Ardhasamavṛtta (अर्धसमवृत्त) or Half-even meters refers to meters where alternate quarters of a verse have the same structure. For example: the 1st quarter is similar to the 3rd quarter, and the 2nd quarter is similar to the 4th quarter.
70/N
An example of an Ardhasamavṛtta meter, specifically Aparavaktra (अपरवक्त्र), is found in the Mālatīmādhava by Bhavabhūti x.com
An example of an Ardhasamavṛtta meter, specifically Aparavaktra (अपरवक्त्र), is found in the Mālatīmādhava by Bhavabhūti x.com
71/N
Viṣamavṛtta (विषमवृत्त) refers to meters in which all the pādas (quarters) differ in the number and placement of syllables. There is no division into genera and species for Viṣamavṛtta meters, as the structure is inherently asymmetrical.
Viṣamavṛtta (विषमवृत्त) refers to meters in which all the pādas (quarters) differ in the number and placement of syllables. There is no division into genera and species for Viṣamavṛtta meters, as the structure is inherently asymmetrical.
73/N
An example of an Viṣamavṛtta meter, specifically Lalitam (ललितम्), is found in the Natyashahstra of Bharata: x.com
An example of an Viṣamavṛtta meter, specifically Lalitam (ललितम्), is found in the Natyashahstra of Bharata: x.com
74/N
In Jāti (जाति) metres, the rhythm is determined by mātrās (syllabic instants) rather than the number of syllables in a quarter (pāda). The most widely known Jati meter is Āryā (आर्या), which has nine varieties. x.com
In Jāti (जाति) metres, the rhythm is determined by mātrās (syllabic instants) rather than the number of syllables in a quarter (pāda). The most widely known Jati meter is Āryā (आर्या), which has nine varieties. x.com
75/N
An example of an Āryā meter, specifically Pathyā, is found in the Natyashahstra of Bharata
(the thread continues...) x.com
An example of an Āryā meter, specifically Pathyā, is found in the Natyashahstra of Bharata
(the thread continues...) x.com
76/N
An important aspect of Chhanda or meter is metrical pause. There are two types of pauses in Sanskrit prosody: Virama (विराम) and Yati (यति)
An important aspect of Chhanda or meter is metrical pause. There are two types of pauses in Sanskrit prosody: Virama (विराम) and Yati (यति)
77/N
In Sanskrit prosody, a sentinel pause or a significant pause in a verse is often referred to as Virama (विराम) x.com
In Sanskrit prosody, a sentinel pause or a significant pause in a verse is often referred to as Virama (विराम) x.com
78/N
In Sanskrit prosody, a Harmonic Pause is known as Yati (यति). It occurs within a quarter (pāda) of a verse after specific syllables, contributing to the rhythm and harmony.
In Sanskrit prosody, a Harmonic Pause is known as Yati (यति). It occurs within a quarter (pāda) of a verse after specific syllables, contributing to the rhythm and harmony.
79/N
Sanskrit prosodians scan a verse and divide it into Gañas (गण) for classification. The arrangement of these Gañas determines the specific metre (e.g., Anuṣṭup, Triṣṭup, etc.)
Sanskrit prosodians scan a verse and divide it into Gañas (गण) for classification. The arrangement of these Gañas determines the specific metre (e.g., Anuṣṭup, Triṣṭup, etc.)
80/N
A Gaña (गण) is composed of three Akshara - each one s either (लघु / Laghu) or long (गुरु / Guru). There are eight major Gañas each with its own syllabic pattern as shown below: x.com
A Gaña (गण) is composed of three Akshara - each one s either (लघु / Laghu) or long (गुरु / Guru). There are eight major Gañas each with its own syllabic pattern as shown below: x.com
81/N
In addition to the standard eight Gañas, there are two special ones Ga (ग गण) and La (ल गण) x.com
In addition to the standard eight Gañas, there are two special ones Ga (ग गण) and La (ल गण) x.com
82/N
This concludes the section on fundamental architectural elements of Chhanda
This concludes the section on fundamental architectural elements of Chhanda
83/N
In this section, we will look into why and how binary representation was invented in ancient India x.com
In this section, we will look into why and how binary representation was invented in ancient India x.com
84/N
In the previous section, I described the core architectural concepts of Chhanda.
In the previous section, I described the core architectural concepts of Chhanda.
85/N
The reason ancient Indian prosodists used a rigorous architecture to tie different aspects of prosody together is so that they can mathematically analyze them
The reason ancient Indian prosodists used a rigorous architecture to tie different aspects of prosody together is so that they can mathematically analyze them
86/N
But robust mathematical analysis of any complex information first requires appropriate robust representation of such information.
But robust mathematical analysis of any complex information first requires appropriate robust representation of such information.
87/N
The ancient Indian prosodists invented binary representation as they found it to be the most effective way to build a foundation for useful and interesting computational methods.
The ancient Indian prosodists invented binary representation as they found it to be the most effective way to build a foundation for useful and interesting computational methods.
88/N
Let’s take a pause here and understand the implication.
Let’s take a pause here and understand the implication.
89/N
Even if we consider Pingala’s Chhanda Shastra as the reference point, it implies that the concept and invention of binary representation originated in ancient India no later than 300 BCE.
Even if we consider Pingala’s Chhanda Shastra as the reference point, it implies that the concept and invention of binary representation originated in ancient India no later than 300 BCE.
90/N
As I mentioned earlier, Pingala’s Chhanda Shastra is a significant contribution within a long tradition of works on prosody in ancient India. Therefore, it is quite possible that binary representation was in use even earlier in ancient India.
As I mentioned earlier, Pingala’s Chhanda Shastra is a significant contribution within a long tradition of works on prosody in ancient India. Therefore, it is quite possible that binary representation was in use even earlier in ancient India.
91/N
In 1679, binary representation was rediscovered by Gottfried Wilhelm Leibniz, a German philosopher, polymath & mathematician He envisioned the binary number system - using only 0s and 1s as a foundation for logical computation.
In 1679, binary representation was rediscovered by Gottfried Wilhelm Leibniz, a German philosopher, polymath & mathematician He envisioned the binary number system - using only 0s and 1s as a foundation for logical computation.
92/N
Binary analysis in Sanskrit prosody relies on recognizing that Laghu (L) and Guru (G) are the two fundamental units of metrical construction.
Binary analysis in Sanskrit prosody relies on recognizing that Laghu (L) and Guru (G) are the two fundamental units of metrical construction.
93/N
Just as modern binary uses 0 and 1 to encode information, Indian prosodists treated G and L as symbols for both abstraction but also for binary representation
Just as modern binary uses 0 and 1 to encode information, Indian prosodists treated G and L as symbols for both abstraction but also for binary representation
94/N
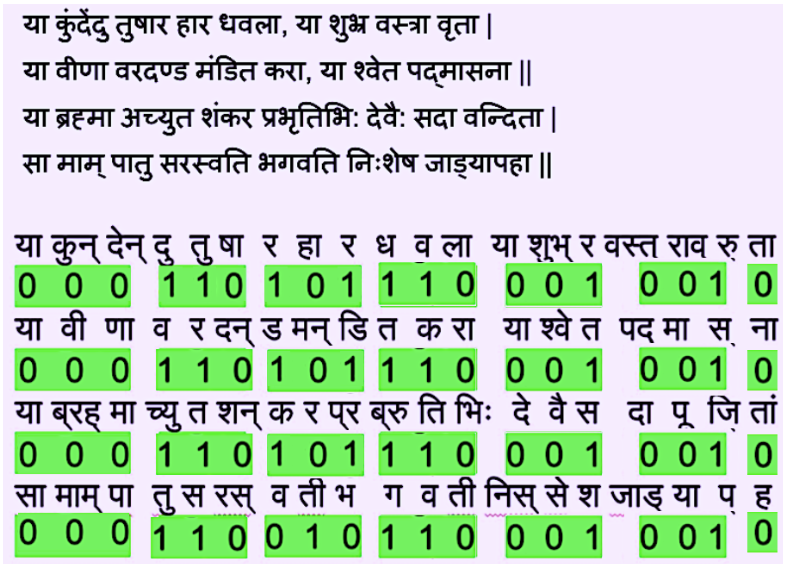
Below I have denoted the individual syllables (अक्षर) of the very popular Saraswati Vandana using 1 and 0 where 1 represents a Guru syllable and 0 represents a Laghu syllable x.com
Below I have denoted the individual syllables (अक्षर) of the very popular Saraswati Vandana using 1 and 0 where 1 represents a Guru syllable and 0 represents a Laghu syllable x.com
95/N
This binary representation enabled Indian prosodists to count syllables, measure weights, and predict combinations systematically.
This binary representation enabled Indian prosodists to count syllables, measure weights, and predict combinations systematically.
96/N
Using this binary encoding, Indian prosodists could create mathematical recipes to generate metrical patterns, calculate permutations, and even validate meter compliance
Using this binary encoding, Indian prosodists could create mathematical recipes to generate metrical patterns, calculate permutations, and even validate meter compliance
97/N
As you will see in this thread later that the binary to decimal conversion method is fully described in Pingala’s Uddiṣṭa Pratyaya
As you will see in this thread later that the binary to decimal conversion method is fully described in Pingala’s Uddiṣṭa Pratyaya
98/N
Similarly Pingala’s Naṣṭa Pratyaya outlines how to convert a decimal number to binary
It’s important to point out a key difference between Pingala’s binary system & modern binary numbers
Similarly Pingala’s Naṣṭa Pratyaya outlines how to convert a decimal number to binary
It’s important to point out a key difference between Pingala’s binary system & modern binary numbers
99/N
In Pingala’s binary representation, the highest-valued positions are arranged on the right, reflecting the sequence of poetic meters.
In Pingala’s binary representation, the highest-valued positions are arranged on the right, reflecting the sequence of poetic meters.
100/N
In contrast, modern binary systems follow the left-to-right positional hierarchy similar to the decimal system developed in India, where the highest-valued digits occupy the leftmost positions.
(the thread continues....)
In contrast, modern binary systems follow the left-to-right positional hierarchy similar to the decimal system developed in India, where the highest-valued digits occupy the leftmost positions.
(the thread continues....)
101/N
This key difference highlights how Pingala’s binary notation was tailored to fit the rhythm and structure of prosody
This key difference highlights how Pingala’s binary notation was tailored to fit the rhythm and structure of prosody
102/N
One of the profound computational topics that ancient Indian mathematician Pingala analyzed was how we can systematically list all the patterns of n syllables for any n. x.com
One of the profound computational topics that ancient Indian mathematician Pingala analyzed was how we can systematically list all the patterns of n syllables for any n. x.com
103/N
In his seminal work “Chhanda Sutra” (no later than 300 BCE), Pingala provides a precise numerical method for listing patterns of n syllables known as प्रस्तार (prastāra or expansion)
In his seminal work “Chhanda Sutra” (no later than 300 BCE), Pingala provides a precise numerical method for listing patterns of n syllables known as प्रस्तार (prastāra or expansion)
104/N
This invention changed the course of human history laying the groundwork for multiple mathematical concepts including binary representation & combinatorics
This invention changed the course of human history laying the groundwork for multiple mathematical concepts including binary representation & combinatorics
105/N
The listing of patterns of n syllables in a table, as described by Pingala in his Chhanda Sutra, served a profound purpose rooted in both poetics and mathematics.
The listing of patterns of n syllables in a table, as described by Pingala in his Chhanda Sutra, served a profound purpose rooted in both poetics and mathematics.
106/N
The patterns were essential for composing and analyzing metrical structures in Sanskrit poetry - an art form that demanded precision, symmetry, and musicality.
The patterns were essential for composing and analyzing metrical structures in Sanskrit poetry - an art form that demanded precision, symmetry, and musicality.
107/N
As explained in one of the previous sections, the rhythm of Sanskrit poetry verses depended on carefully arranged sequences of long (Guru) and short (Laghu) syllables.
As explained in one of the previous sections, the rhythm of Sanskrit poetry verses depended on carefully arranged sequences of long (Guru) and short (Laghu) syllables.
108/N
These patterns not only ensured aesthetic harmony but also preserved oral traditions by aiding memorization.
These patterns not only ensured aesthetic harmony but also preserved oral traditions by aiding memorization.
109/N
The prastāra table provided poets, scholars, and reciters with a systematic tool to explore and catalog all possible rhythmic combinations, ensuring that every conceivable meter could be identified, constructed, or analyzed.
The prastāra table provided poets, scholars, and reciters with a systematic tool to explore and catalog all possible rhythmic combinations, ensuring that every conceivable meter could be identified, constructed, or analyzed.
110/N
Beyond poetry, Pingala’s combinatorial method established principles in mathematics and information theory. It exemplified algorithmic thinking - laying the groundwork for developments in binary arithmetic, combinatorics, and coding systems.
Beyond poetry, Pingala’s combinatorial method established principles in mathematics and information theory. It exemplified algorithmic thinking - laying the groundwork for developments in binary arithmetic, combinatorics, and coding systems.
111/N
From what follows it will be clear that by prastāra, Pingala is talking about the matrix showing all possible combinations of 0s and 1s in n digit binary numbers.
From what follows it will be clear that by prastāra, Pingala is talking about the matrix showing all possible combinations of 0s and 1s in n digit binary numbers.
112/N
We know that there are 2ⁿ possible combinations of n digit binary numbers. So when we write all possible combinations, it will result in a matrix of dimension 2ⁿ by n
We know that there are 2ⁿ possible combinations of n digit binary numbers. So when we write all possible combinations, it will result in a matrix of dimension 2ⁿ by n
114/N
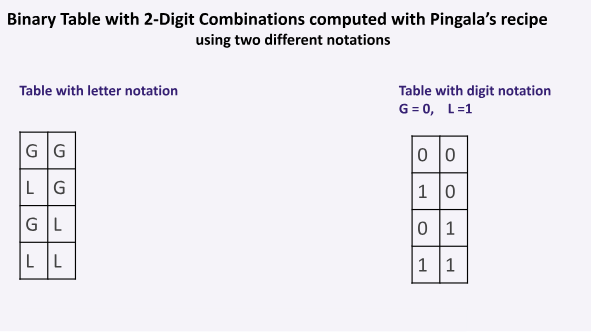
Pingala’s sutra 8:20 specifies that the expansion (prastara) for one syllable (akshara) will contain either of two elements: a long syllable (G) or a short syllable (L). We can also represent the same table with modern notation with G=0 and L =1.
Pingala’s sutra 8:20 specifies that the expansion (prastara) for one syllable (akshara) will contain either of two elements: a long syllable (G) or a short syllable (L). We can also represent the same table with modern notation with G=0 and L =1.
116/N
Pingala’s sutra 8:21 specifies that to compute the the expansion (prastāra) of two syllables (akshara), we need to mix the previous 1 syllable prastāra with itself
Pingala’s sutra 8:21 specifies that to compute the the expansion (prastāra) of two syllables (akshara), we need to mix the previous 1 syllable prastāra with itself
117/N
Below I am showing how to generate a binary table of 2 digit combinations using Pinagala’s recipe. x.com
Below I am showing how to generate a binary table of 2 digit combinations using Pinagala’s recipe. x.com
118/N
We can assign the value 0 to G and 1 to L. The resulting tables are shown below. The table in the right is very similar to what is used in modern binary notation x.com
We can assign the value 0 to G and 1 to L. The resulting tables are shown below. The table in the right is very similar to what is used in modern binary notation x.com
119/N
In modern notation all possible 2 digit binary numbers are depicted in ascending order of their magnitude, as shown below in the 2 by 2 matrix x.com
In modern notation all possible 2 digit binary numbers are depicted in ascending order of their magnitude, as shown below in the 2 by 2 matrix x.com
120/N
Ancient Indians preferred the notation shown in the left compared to the modern notation in right because of the prevalent practice of writing from left to right. The characters uttered first are written to the left of those who are uttered later. x.com
Ancient Indians preferred the notation shown in the left compared to the modern notation in right because of the prevalent practice of writing from left to right. The characters uttered first are written to the left of those who are uttered later. x.com
121/N
It’s interesting to note that in the previous diagram, the table on the right is a mirror image of the table on the left.
It’s interesting to note that in the previous diagram, the table on the right is a mirror image of the table on the left.
122/N
Pingala’s sutra 8.23 explains that to get expansion of 3 binary numbers, we need to again mix G & L separately with the prastāra of 2 syllables. The method involves appending G to the end of each pattern from the two-syllable expansion, & then repeating the process with L.
Pingala’s sutra 8.23 explains that to get expansion of 3 binary numbers, we need to again mix G & L separately with the prastāra of 2 syllables. The method involves appending G to the end of each pattern from the two-syllable expansion, & then repeating the process with L.
123/N
Below I am showing how to generate a binary table of 3 digit combinations using Pinagala’s recipe. x.com
Below I am showing how to generate a binary table of 3 digit combinations using Pinagala’s recipe. x.com
124/N
Let's show the final 8 by 3 binary table as computed using Pingala’s rules using three different notations. x.com
Let's show the final 8 by 3 binary table as computed using Pingala’s rules using three different notations. x.com
125/N
Once again, note that in the previous diagram, the rightmost table (what we typically view as a modern binary table of 3 digits) is a mirror image of Pingala’s table in the middle.
(the thread continues...)
Once again, note that in the previous diagram, the rightmost table (what we typically view as a modern binary table of 3 digits) is a mirror image of Pingala’s table in the middle.
(the thread continues...)
126/N
Pingala’s sutra 8.23 notes that there are exactly eight patterns for three syllables.
Pingala’s sutra 8.23 notes that there are exactly eight patterns for three syllables.
128/N
The rules given by Pingala generalize elegantly, offering a recursive framework to construct binary syllable patterns of arbitrary length.
The rules given by Pingala generalize elegantly, offering a recursive framework to construct binary syllable patterns of arbitrary length.
129/N
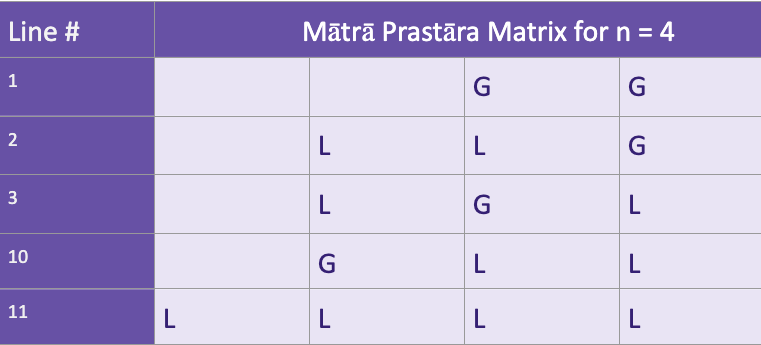
Pingala is not the only mathematician in the ancient Indian lineage who provided a recipe for building tables of binary combinations with n-bits. Kedarabhatta, another Hindu mathematical genius provided a completely different recipe no later than 1000 CE x.com
Pingala is not the only mathematician in the ancient Indian lineage who provided a recipe for building tables of binary combinations with n-bits. Kedarabhatta, another Hindu mathematical genius provided a completely different recipe no later than 1000 CE x.com
130/N
Kedarabhatta in his magnificent work titled Vrittaratnākara provided the following numerical recipe to get the expansion / prastāra of a binary table for a given number of bits x.com
Kedarabhatta in his magnificent work titled Vrittaratnākara provided the following numerical recipe to get the expansion / prastāra of a binary table for a given number of bits x.com
133/N
Below I am showing the final 16 by 4 binary table as computed using Kdarabhatta’s rules using three different notations. x.com
Below I am showing the final 16 by 4 binary table as computed using Kdarabhatta’s rules using three different notations. x.com
134/N
Once again, note that in the previous diagram, the rightmost table (what we typically view as a modern binary table of 4 digits) is a mirror image of Kedarabhatta’s table in the middle.
Once again, note that in the previous diagram, the rightmost table (what we typically view as a modern binary table of 4 digits) is a mirror image of Kedarabhatta’s table in the middle.
135/N
When we contrast Pingala's method with Kedarabatta’s, it becomes evident that Pingala employs a recursive approach, while Kedarabatta adopts an iterative strategy.
When we contrast Pingala's method with Kedarabatta’s, it becomes evident that Pingala employs a recursive approach, while Kedarabatta adopts an iterative strategy.
136/N
Imagine we have a table / matrix of binary patterns of n syllables. For some reason, one of the patterns is erased from the list. How can we recover the missing pattern? x.com
Imagine we have a table / matrix of binary patterns of n syllables. For some reason, one of the patterns is erased from the list. How can we recover the missing pattern? x.com
137/N
As an example, recall the binary table of 4 digits that we computed using Kedarabhatta’s recipe. Imagine now, the 5th row is missing from that table. x.com
As an example, recall the binary table of 4 digits that we computed using Kedarabhatta’s recipe. Imagine now, the 5th row is missing from that table. x.com
138/N
How do we recover just the 5th row for the above table, without recomputing the whole table ? Pingala provides compact rules for recovering such information in chapter 8 of his Chhanda Sutra x.com
How do we recover just the 5th row for the above table, without recomputing the whole table ? Pingala provides compact rules for recovering such information in chapter 8 of his Chhanda Sutra x.com
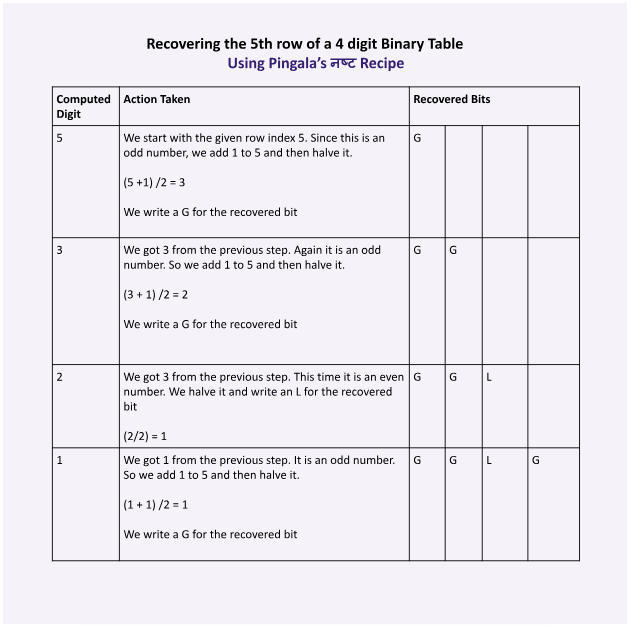
140/N
Below I have shown how to cover the 5the row of a binary table of 4-digit combinations. As you can see the recovered row is “G G L G” x.com
Below I have shown how to cover the 5the row of a binary table of 4-digit combinations. As you can see the recovered row is “G G L G” x.com
141/N
Pingala’s verses 8.24 and 8.25 which describe the Naṣṭa recipe are essentially a recipe for converting a decimal number to its binary equivalent
Pingala’s verses 8.24 and 8.25 which describe the Naṣṭa recipe are essentially a recipe for converting a decimal number to its binary equivalent
142/N
However there are two subtle differences between the Pingala's Naṣṭa method and the modern method representation of binary numbers.
However there are two subtle differences between the Pingala's Naṣṭa method and the modern method representation of binary numbers.
143/N
Difference # 1: In Pingala's system the numbers are written with the higher place value digits to the right of lower place value digits.
Difference # 1: In Pingala's system the numbers are written with the higher place value digits to the right of lower place value digits.
144/N
Difference #2: In Pingala’s method the index starts with 1, whereas in modern binary representation the index starts from 0.
Difference #2: In Pingala’s method the index starts with 1, whereas in modern binary representation the index starts from 0.
145/N
Below I am providing a handy Python class that implements Pingala’s Naṣṭa recipe to do a conversion from decimal to binary x.com
Below I am providing a handy Python class that implements Pingala’s Naṣṭa recipe to do a conversion from decimal to binary x.com
146/N
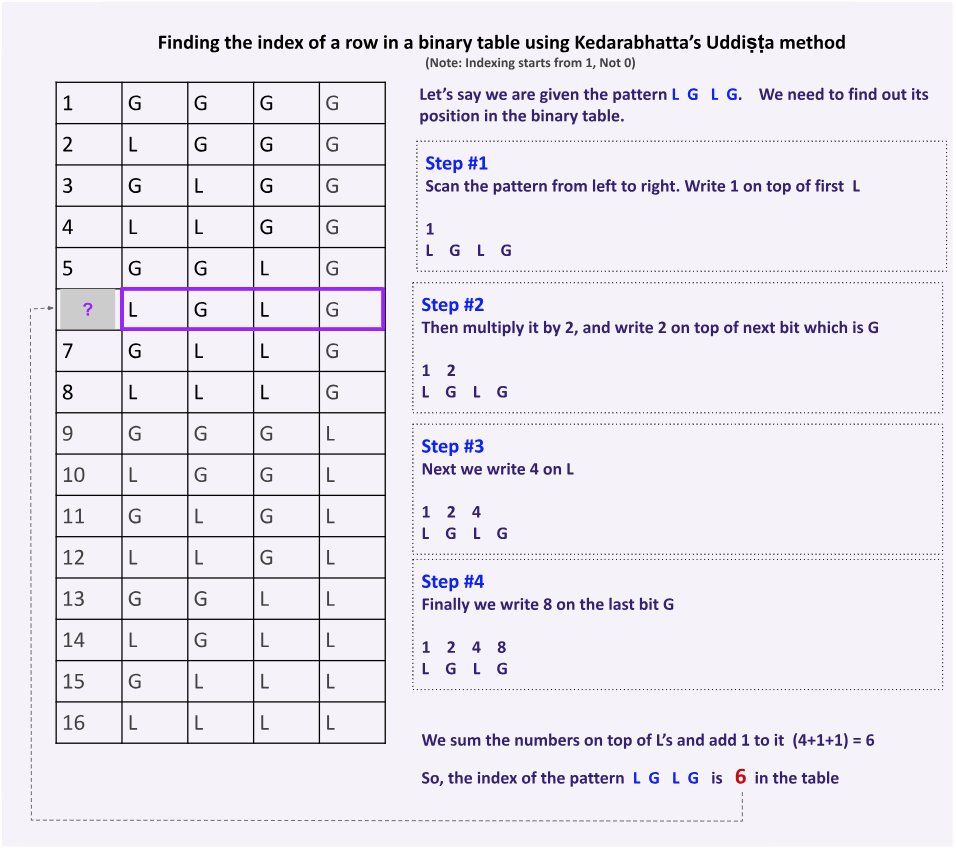
Next problem Pingala focused on is: Given any pattern, how can we find its position on the list without recreating the entire list? x.com
Next problem Pingala focused on is: Given any pattern, how can we find its position on the list without recreating the entire list? x.com
147/N
Pingala’s indexing process essentially reverses the recipe he developed for Nasta.
Pingala’s indexing process essentially reverses the recipe he developed for Nasta.
150/N
Let’s take an example to illustrate the Uddiṣṭa method. In this example, we are given the pattern “G L G L”. We need to find out its position in the binary table.
(the thread continues...) x.com
Let’s take an example to illustrate the Uddiṣṭa method. In this example, we are given the pattern “G L G L”. We need to find out its position in the binary table.
(the thread continues...) x.com
151/N
If you look closely, you will find that Pingala’s Uddiṣṭa method is an algorithm to find the decimal equivalent of a binary number. Let me provide the recursive recipe for this following Pingala’s footsteps x.com
If you look closely, you will find that Pingala’s Uddiṣṭa method is an algorithm to find the decimal equivalent of a binary number. Let me provide the recursive recipe for this following Pingala’s footsteps x.com
152/N
Kedarabhatta gave a different algorithm for Uddiṣṭa in order to compute the index of binary pattern (or equivalently to convert a binary string to a decimal number) x.com
Kedarabhatta gave a different algorithm for Uddiṣṭa in order to compute the index of binary pattern (or equivalently to convert a binary string to a decimal number) x.com
155/N
Next we are going to focus on an important problem that ancient Indians solved in the field of combinatorics. x.com
Next we are going to focus on an important problem that ancient Indians solved in the field of combinatorics. x.com
156/N
Suppose we have a 6 syllable meter and we want to know how many of its combinations have 2 Laghu (short) syllables or equivalently 4 Guru (long) syllables
Suppose we have a 6 syllable meter and we want to know how many of its combinations have 2 Laghu (short) syllables or equivalently 4 Guru (long) syllables
157/N
Lagakriya (लगक्रिया) is the method that provides a solution to these type problems. It essentially computed how many different ways we can choose r objects from n of them (n > r). The modern notation used for Lagakriya is nCr
Lagakriya (लगक्रिया) is the method that provides a solution to these type problems. It essentially computed how many different ways we can choose r objects from n of them (n > r). The modern notation used for Lagakriya is nCr
158/N
Pingala gave a very terse method for computing nCr in the Chhanda Sutra. Without additional commentary, it is hard to decode this. x.com
Pingala gave a very terse method for computing nCr in the Chhanda Sutra. Without additional commentary, it is hard to decode this. x.com
159/N
But, we are in luck, as another genius Hindu mathematician named Halayudha Bhatta did exactly that. x.com
But, we are in luck, as another genius Hindu mathematician named Halayudha Bhatta did exactly that. x.com
160/N
Halayudha Bhatta wrote a commentary called Mritasanjeevani (no later than 10th century CE) on Pinagala’s Chhanda Sutra
Halayudha Bhatta wrote a commentary called Mritasanjeevani (no later than 10th century CE) on Pinagala’s Chhanda Sutra
161/N
In Mritasanjeevani, Halayudha analyzed Pinagal’s Lagakriya sutra in detail and showed how to create a table of numbers called मेरु प्रस्तार (Meru Prastara). मेरु प्रस्तार literally means an expanded mountain. The reason behind the name will be clear in the analysis below
In Mritasanjeevani, Halayudha analyzed Pinagal’s Lagakriya sutra in detail and showed how to create a table of numbers called मेरु प्रस्तार (Meru Prastara). मेरु प्रस्तार literally means an expanded mountain. The reason behind the name will be clear in the analysis below
163/N
Halayudha's Meru Prastara, documented no later than 10th century CE, laid the foundation for combinatorics and binomial coefficients - concepts that re-emerged in Europe nearly 700 years later as Pascal's Triangle.
Halayudha's Meru Prastara, documented no later than 10th century CE, laid the foundation for combinatorics and binomial coefficients - concepts that re-emerged in Europe nearly 700 years later as Pascal's Triangle.
164/N
It is interesting to note that the French mathematician Blaise Pascal did not invent the triangle named after him; he popularized it in Europe through his work "Traité du triangle arithmétique" (Treatise on the Arithmetical Triangle) published in 1654.
It is interesting to note that the French mathematician Blaise Pascal did not invent the triangle named after him; he popularized it in Europe through his work "Traité du triangle arithmétique" (Treatise on the Arithmetical Triangle) published in 1654.
165/N
Let’s analyze Halayudha’s commentary on Meru Prastara verse by verse starting with the first verse x.com
Let’s analyze Halayudha’s commentary on Meru Prastara verse by verse starting with the first verse x.com
166/N
Halayudha’s first verse gives us a method to build a pyramid-like pattern starting with a single square and adding rows, incrementing by one square per row, each extending halfway outward x.com
Halayudha’s first verse gives us a method to build a pyramid-like pattern starting with a single square and adding rows, incrementing by one square per row, each extending halfway outward x.com
168/N
In the second verse Halayudha's instructs us to start with 1 in the only square of the first row, followed by 1s in each square of the second row, and 1s at the extreme squares of every subsequent row. x.com
In the second verse Halayudha's instructs us to start with 1 in the only square of the first row, followed by 1s in each square of the second row, and 1s at the extreme squares of every subsequent row. x.com
170/N
Halayudha's third verse completed the mountain / pyramid. He asks us to start with 3s in the second row's middle squares. Each subsequent row is filled by summing the two squares directly above, representing binomial coefficients x.com
Halayudha's third verse completed the mountain / pyramid. He asks us to start with 3s in the second row's middle squares. Each subsequent row is filled by summing the two squares directly above, representing binomial coefficients x.com
172/N
In the fourth verse, Halayudha explains that the mountain or triangle represents a combinatorial framework for arranging syllables, capturing all possible patterns of short and long syllables x.com
In the fourth verse, Halayudha explains that the mountain or triangle represents a combinatorial framework for arranging syllables, capturing all possible patterns of short and long syllables x.com
173/N
Kedarabhatta in his seminal work Vrittaratnākara also provides specific rules to get the number of combinations of laghu (L) and Guru (L) symbols among all possible combinations of n symbols. x.com
Kedarabhatta in his seminal work Vrittaratnākara also provides specific rules to get the number of combinations of laghu (L) and Guru (L) symbols among all possible combinations of n symbols. x.com
174/N
The verses from Kedarabhatta’s Vrittaratnākara to calculate nCr are provided below. His method is slightly different from that of Halayudha x.com
The verses from Kedarabhatta’s Vrittaratnākara to calculate nCr are provided below. His method is slightly different from that of Halayudha x.com
175/N
Below I am giving a modern translation of Kedarabhatta’s verses to compute nCr along with an illustration for the case of n = 6
(the thread continues...) x.com
Below I am giving a modern translation of Kedarabhatta’s verses to compute nCr along with an illustration for the case of n = 6
(the thread continues...) x.com
176/N
Bhāskarāchārya(1114–1185 CE), the legendary Indian mathematician and astronomer, was centuries ahead of his time. His masterpiece Lilavati dazzled with arithmetic brilliance, while Bijaganita explored algebra like never before. x.com
Bhāskarāchārya(1114–1185 CE), the legendary Indian mathematician and astronomer, was centuries ahead of his time. His masterpiece Lilavati dazzled with arithmetic brilliance, while Bijaganita explored algebra like never before. x.com
177/N
In addition to other mathematical gems, Bhāskarāchārya also provided a cool method for computing binomial coefficients in his seminal work Lilavati x.com
In addition to other mathematical gems, Bhāskarāchārya also provided a cool method for computing binomial coefficients in his seminal work Lilavati x.com
178/N
Below I am providing translation for the above verses from Lilavati that enables us to compute nCr x.com
Below I am providing translation for the above verses from Lilavati that enables us to compute nCr x.com
179/N
'Sankhyā' stands for the number of possible combinations of n bits. Both Pingala and Kedarabhatta provided methods to compute 2ⁿ x.com
'Sankhyā' stands for the number of possible combinations of n bits. Both Pingala and Kedarabhatta provided methods to compute 2ⁿ x.com
180/N
Let’s first see how Pingala addressed computation of 2ⁿ. Below I am providing the sutras from Chapter 8 of Chhanda Sutra x.com
Let’s first see how Pingala addressed computation of 2ⁿ. Below I am providing the sutras from Chapter 8 of Chhanda Sutra x.com
181/N
Below I am providing translation of the above sutras along with an example
(side note: notice the usage of zero or shunya. It is one of the earliest mention of zero in the world) x.com
Below I am providing translation of the above sutras along with an example
(side note: notice the usage of zero or shunya. It is one of the earliest mention of zero in the world) x.com
183/N
Kedarabhatta in his seminal work Vrittaratnākara gave a very different approach to compute 2ⁿ x.com
Kedarabhatta in his seminal work Vrittaratnākara gave a very different approach to compute 2ⁿ x.com
185/N
Fibonacci numbers are one of the most elegant and fascinating sequences in mathematics, revealing patterns that echo throughout nature, art, and science. x.com
Fibonacci numbers are one of the most elegant and fascinating sequences in mathematics, revealing patterns that echo throughout nature, art, and science. x.com
186/N
It was in ancient India that this Fibonacci sequence was discovered. In fact, there has been a long tradition of mathematically analyzing this sequence in India in the context of prosody
It was in ancient India that this Fibonacci sequence was discovered. In fact, there has been a long tradition of mathematically analyzing this sequence in India in the context of prosody
187/N
Ancient Indian mathematician Virahāṅka discovered this sequence at least 500 years before Fibonacci. Another Indian mathematician Hemachandra traced this sequence to the works of Pingala which dates back to at least 300 BCE
Ancient Indian mathematician Virahāṅka discovered this sequence at least 500 years before Fibonacci. Another Indian mathematician Hemachandra traced this sequence to the works of Pingala which dates back to at least 300 BCE
188/N
Before we go into the details of the sequence, let’s talk about what exactly Fibonacci sequence is
Before we go into the details of the sequence, let’s talk about what exactly Fibonacci sequence is
189/N
This sequence begins with 0 and 1, followed by 1, 2, 3, 5, 8, 13, 21, and so on, where each number is the sum of the two preceding ones.
This sequence begins with 0 and 1, followed by 1, 2, 3, 5, 8, 13, 21, and so on, where each number is the sum of the two preceding ones.
190/N
Mathematically, the sequence is defined by the formula Fₙ = Fₙ₋₁ + Fₙ₋₂ for n >= 0 with the initial conditions F₀ = 0 and F₁=1
Mathematically, the sequence is defined by the formula Fₙ = Fₙ₋₁ + Fₙ₋₂ for n >= 0 with the initial conditions F₀ = 0 and F₁=1
191/N
Fibonacci numbers appear widely in nature, such as in the spirals of shells, seed arrangements in flowers, and the branching of trees.
Fibonacci numbers appear widely in nature, such as in the spirals of shells, seed arrangements in flowers, and the branching of trees.
192/N
They have inspired applications across disciplines, including art, architecture, music, and computer algorithms, showcasing their deep mathematical significance.
They have inspired applications across disciplines, including art, architecture, music, and computer algorithms, showcasing their deep mathematical significance.
193/N
Remarkably, the ratio of consecutive Fibonacci numbers approaches the Golden Ratio (𝜙 ≈ 1.618), a constant celebrated for its connection to beauty and harmony.
Remarkably, the ratio of consecutive Fibonacci numbers approaches the Golden Ratio (𝜙 ≈ 1.618), a constant celebrated for its connection to beauty and harmony.
194/N
The Fibonacci numbers are embedded within Pascal’s Triangle. When the diagonals of Pascal’s Triangle (which was also invented in India as shown in this thread) are summed, they form Fibonacci numbers.
The Fibonacci numbers are embedded within Pascal’s Triangle. When the diagonals of Pascal’s Triangle (which was also invented in India as shown in this thread) are summed, they form Fibonacci numbers.
195/N
Named after the Italian mathematician Leonardo of Pisa, known as Fibonacci, these numbers were introduced to Europe in his book Liber Abaci published in 1202 CE
Named after the Italian mathematician Leonardo of Pisa, known as Fibonacci, these numbers were introduced to Europe in his book Liber Abaci published in 1202 CE
196/N
It is important to point out the deep impact of Indian mathematics on Fibonacci’s work. I am providing an excerpt written by Fibonacci from the book “Liber Abaci” x.com
It is important to point out the deep impact of Indian mathematics on Fibonacci’s work. I am providing an excerpt written by Fibonacci from the book “Liber Abaci” x.com
197/N
Fibonacci acknowledged India as the origin of a profound mathematical system (including its decimal system), noting its use among Egyptians, Syrians, Greeks, and Sicilians.
Fibonacci acknowledged India as the origin of a profound mathematical system (including its decimal system), noting its use among Egyptians, Syrians, Greeks, and Sicilians.
198/N
Recognizing its superiority over older, error-prone methods, Fibonacci mentioned that he adopted the Indian mathematical approach with insights from Euclidean geometry x.com
Recognizing its superiority over older, error-prone methods, Fibonacci mentioned that he adopted the Indian mathematical approach with insights from Euclidean geometry x.com
199/N
From now on, we will refer to the Fibonacci sequence as the Virahāṅka-Hemachandra sequence, honoring the rich legacy of Indian mathematicians and prosodists who originally discovered it.
From now on, we will refer to the Fibonacci sequence as the Virahāṅka-Hemachandra sequence, honoring the rich legacy of Indian mathematicians and prosodists who originally discovered it.
200/N
Today what we know as Fibonacci sequence was originally discovered by the great Indian mathematician Virahāṅka (no later than 600 CE) & elaborated later by another genius mathematician Hemachandra (no later than 1100 CE)
(the thread continues...) x.com
Today what we know as Fibonacci sequence was originally discovered by the great Indian mathematician Virahāṅka (no later than 600 CE) & elaborated later by another genius mathematician Hemachandra (no later than 1100 CE)
(the thread continues...) x.com
201/N
Virahanka (विरहाङ्क) was a brilliant Indian prosodist and mathematician. He is believed to have composed his seminal work Vrattajati Samuccaya (वृत्तजातिसमुच्चय:) no later than 600 CE.
Virahanka (विरहाङ्क) was a brilliant Indian prosodist and mathematician. He is believed to have composed his seminal work Vrattajati Samuccaya (वृत्तजातिसमुच्चय:) no later than 600 CE.
202/N
Virahanka’s contributions to prosody expanded upon Pingala’s Chhanda-sutras (no later than 300 BCE). His work later served as the foundation for Gopala’s 12th-century commentary.
Virahanka’s contributions to prosody expanded upon Pingala’s Chhanda-sutras (no later than 300 BCE). His work later served as the foundation for Gopala’s 12th-century commentary.
203/N
So far in this thread we have worked with meters that are of type "Varna Vritta". It refers to a meter based on the specific arrangement of letters (varnas), where the pattern of light (Laghu) and heavy (Guru) syllables within a line is predetermined
So far in this thread we have worked with meters that are of type "Varna Vritta". It refers to a meter based on the specific arrangement of letters (varnas), where the pattern of light (Laghu) and heavy (Guru) syllables within a line is predetermined
204/N
"Matra Vritta" refers to a meter based on the duration of syllables (morae), where the number of "matras" (metrical units) in a line is fixed, with the syllable count also being important.
"Matra Vritta" refers to a meter based on the duration of syllables (morae), where the number of "matras" (metrical units) in a line is fixed, with the syllable count also being important.
205/N
Matra Vritta focuses on the timing of syllables, while Varna Vritta focuses on the specific letter combinations used in a line
Matra Vritta focuses on the timing of syllables, while Varna Vritta focuses on the specific letter combinations used in a line
206/N
Virahanka-Hemachandra sequence is related to the concept of Matra Vritta
Virahanka-Hemachandra sequence is related to the concept of Matra Vritta
207/N
Matra Vritta which enables metrical poetry based on syllabic duration was briefly touched upon by Pingala in the context of Arya and Vaitaliya meters. However, it gained prominence in Prakrit and regional Indian languages.
Matra Vritta which enables metrical poetry based on syllabic duration was briefly touched upon by Pingala in the context of Arya and Vaitaliya meters. However, it gained prominence in Prakrit and regional Indian languages.
208/N
Virahanka (विरहाङ्क) provided a comprehensive explanation of matra vrittas in his work Vrittajati Samuccaya (वृत्तजातिसमुच्चय:). He introduced mathematical techniques to list and count meters based on matras.
Virahanka (विरहाङ्क) provided a comprehensive explanation of matra vrittas in his work Vrittajati Samuccaya (वृत्तजातिसमुच्चय:). He introduced mathematical techniques to list and count meters based on matras.
209/N
The key question Virahanka addressed in this regard was “How many poetic meters are possible for a quarter having n matras? And how can we list all such meters?”
The key question Virahanka addressed in this regard was “How many poetic meters are possible for a quarter having n matras? And how can we list all such meters?”
210/N
Below I am providing the sutras from Vrittajati Samuccaya that deal with the solution to this above problem. The method is called Mātrā Prastāra (मात्रा प्रस्तार) x.com
Below I am providing the sutras from Vrittajati Samuccaya that deal with the solution to this above problem. The method is called Mātrā Prastāra (मात्रा प्रस्तार) x.com
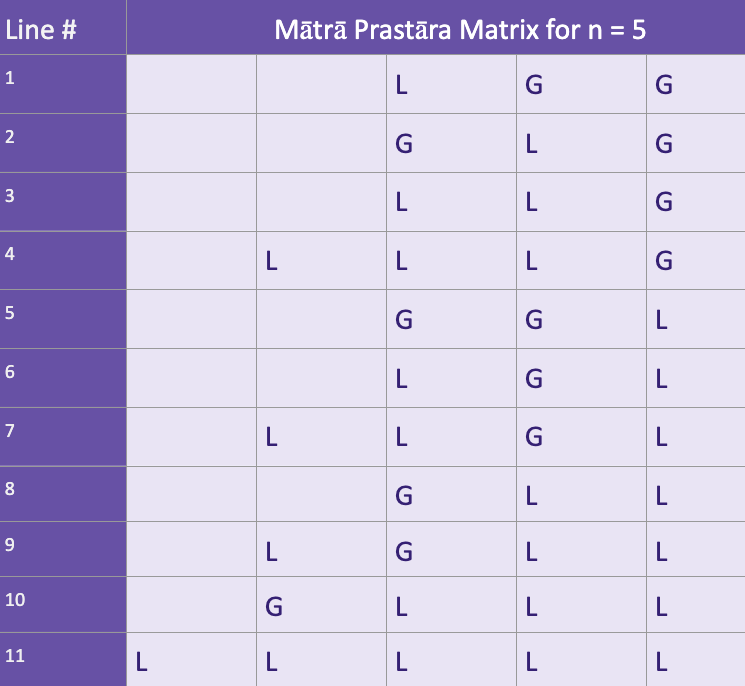
213/N
Now let’s construct a Mātrā Prastāra for a quarter having 5 matras using Virahanka’s method x.com
Now let’s construct a Mātrā Prastāra for a quarter having 5 matras using Virahanka’s method x.com
214/N
Finally let’s construct a Mātrā Prastāra for a quarter having 6 matras using Virahanka’s method x.com
Finally let’s construct a Mātrā Prastāra for a quarter having 6 matras using Virahanka’s method x.com
215/N
Let’s closely observe how the Mātrā Prastāra unfolds when n = 6. The last column of the first 5 rows (rows 1–5) contains all G
Let’s closely observe how the Mātrā Prastāra unfolds when n = 6. The last column of the first 5 rows (rows 1–5) contains all G
216/N
Since the value of G = 2, the remaining columns in these rows must add up to 4 matras.
Since the value of G = 2, the remaining columns in these rows must add up to 4 matras.
217/N
The remaining columns must follow the Prastāra for n = 4 matras. When you compare with the Prastāra table for n = 4, you’ll find that it exactly matches.
The remaining columns must follow the Prastāra for n = 4 matras. When you compare with the Prastāra table for n = 4, you’ll find that it exactly matches.
218/N
Now let’s analyze rows 6 to 13. The last column here contains all Ls. Since the value of L = 1, the remaining columns in these rows must add up to 5 matras.
Now let’s analyze rows 6 to 13. The last column here contains all Ls. Since the value of L = 1, the remaining columns in these rows must add up to 5 matras.
219/N
This means the remaining columns must follow the Prastāra for n = 5 matras. When you compare with the Prastāra table for n = 4, you’ll find that it exactly matches.
This means the remaining columns must follow the Prastāra for n = 5 matras. When you compare with the Prastāra table for n = 4, you’ll find that it exactly matches.
220/N
So, how do we count the total number of poetic meters for n = 6 matras? For n = 6, we observe:
S₆ = S₅ + S₄
So, how do we count the total number of poetic meters for n = 6 matras? For n = 6, we observe:
S₆ = S₅ + S₄
221/N
For any Prastāra with n matras, rows end with either:
G (2 matras) - Remaining columns must add up to n - 2.
Or
L (1 matra) - Remaining columns must add up to n - 1.
For any Prastāra with n matras, rows end with either:
G (2 matras) - Remaining columns must add up to n - 2.
Or
L (1 matra) - Remaining columns must add up to n - 1.
222/N
This leads to a beautiful recurrence relation: Sₙ = Sₙ₋₁ + Sₙ₋₂
Does this remind you of something? Yes, it’s the Fibonacci sequence hidden in poetry!
This leads to a beautiful recurrence relation: Sₙ = Sₙ₋₁ + Sₙ₋₂
Does this remind you of something? Yes, it’s the Fibonacci sequence hidden in poetry!
223/N
Virahanka explained this in his Sankhya Pratyay as follows and he identifies the numbers in the series as simply “Sankhyanka”
Virahanka explained this in his Sankhya Pratyay as follows and he identifies the numbers in the series as simply “Sankhyanka”
224/N
This gives us the following sequence of Virahanka’s Sankhyankas (सङ्ख्यांक) as a function of n x.com
This gives us the following sequence of Virahanka’s Sankhyankas (सङ्ख्यांक) as a function of n x.com
225/N
This gives us the following sequence of Virahanka’s Sankhyankas (सङ्ख्यांक) as a function of n
(the thread continues...) x.com
This gives us the following sequence of Virahanka’s Sankhyankas (सङ्ख्यांक) as a function of n
(the thread continues...) x.com
226/N
Hemacandra, one of the greatest Indian Jaina mathematicians, provided in-depth analysis of the numbers of variations of mātrā-vṛttas in his brilliant book Chandonuśāsana (no later than 1140 CE)
Hemacandra, one of the greatest Indian Jaina mathematicians, provided in-depth analysis of the numbers of variations of mātrā-vṛttas in his brilliant book Chandonuśāsana (no later than 1140 CE)
227/N
Like Virahanka, rather than counting meters based on a fixed number of syllables, Hemachandra analyzed meters with a fixed duration, assigning one beat to short syllables and two beats to long syllables
Like Virahanka, rather than counting meters based on a fixed number of syllables, Hemachandra analyzed meters with a fixed duration, assigning one beat to short syllables and two beats to long syllables
228/N
The number of possible patterns follows the sequence 1, 2, 3, 5, 8, 13, 21. . ., where each term is obtained by summing the two preceding terms.
The number of possible patterns follows the sequence 1, 2, 3, 5, 8, 13, 21. . ., where each term is obtained by summing the two preceding terms.
229/N
Here is an excerpt from chapter 8, section 16 & 17 from Chandonuśāsana by Hemachandra that provides description of how to analyze mātrā-vṛttas and in the process documents the numbers that is today known as Fibonacci sequence x.com
Here is an excerpt from chapter 8, section 16 & 17 from Chandonuśāsana by Hemachandra that provides description of how to analyze mātrā-vṛttas and in the process documents the numbers that is today known as Fibonacci sequence x.com
230/N
The 'Prākṛita-Paiṅgalaṃ' (composed no later than 1300 CE) is one of the most important documents on Prosody which is well known for its comprehensive treatment of Prākṛit and Apabhraṃśa meters, recording not only their definitions, but also copious illustrations
The 'Prākṛita-Paiṅgalaṃ' (composed no later than 1300 CE) is one of the most important documents on Prosody which is well known for its comprehensive treatment of Prākṛit and Apabhraṃśa meters, recording not only their definitions, but also copious illustrations
231/N
Prākṛita-Paiṅgalaṃ shows the connection between Virahanka-Hemachandra numbers & Pingala’s Meru Prastāra.
Prākṛita-Paiṅgalaṃ shows the connection between Virahanka-Hemachandra numbers & Pingala’s Meru Prastāra.
232/N
The author of Prākṛita-Paiṅgalaṃ demonstrated that the Virahanka-Hemachandra numbers are, in fact, sums of numbers on certain diagonals in the Meru Prastāra computed by Pingala x.com
The author of Prākṛita-Paiṅgalaṃ demonstrated that the Virahanka-Hemachandra numbers are, in fact, sums of numbers on certain diagonals in the Meru Prastāra computed by Pingala x.com
233/N
We will now look into brilliant work done by Nārāyaṇa Paṇḍita (1356 CE) in the field of Prosody. x.com
We will now look into brilliant work done by Nārāyaṇa Paṇḍita (1356 CE) in the field of Prosody. x.com
234/N
Nārāyaṇa Paṇḍita was a renowned mathematician of medieval India, celebrated for his profound contributions to arithmetic, algebra, and combinatorics.
Nārāyaṇa Paṇḍita was a renowned mathematician of medieval India, celebrated for his profound contributions to arithmetic, algebra, and combinatorics.
235/N
His masterpiece, Gaṇitakaumudī (The Moonlight of Mathematics), revolutionized combinatorics by generalizing earlier works on permutations, combinations, and enumerations, bridging practical applications with abstract mathematical principles.
His masterpiece, Gaṇitakaumudī (The Moonlight of Mathematics), revolutionized combinatorics by generalizing earlier works on permutations, combinations, and enumerations, bridging practical applications with abstract mathematical principles.
236/N
Complementing this, his Bījagaṇita Vātāṃsa (The Garland of Algebra) delved into algebraic equations and indeterminate analysis, showcasing his deep mathematical insight.
Complementing this, his Bījagaṇita Vātāṃsa (The Garland of Algebra) delved into algebraic equations and indeterminate analysis, showcasing his deep mathematical insight.
237/N
Nārāyaṇa Paṇḍita deserves a special mention in this thread because he treated the combinatorics problems with a broad mathematical viewpoint, generalizing and unifying many of the earlier results.
Nārāyaṇa Paṇḍita deserves a special mention in this thread because he treated the combinatorics problems with a broad mathematical viewpoint, generalizing and unifying many of the earlier results.
238/N
Specifically, Nārāyaṇa Paṇḍita considered prastāras of syllabic meters with more than two types of syllables generalising the work of Piṅgala, prastāras of permutations with repetitions generalising the work of Śārṅgadeva on svara-prastāra
Specifically, Nārāyaṇa Paṇḍita considered prastāras of syllabic meters with more than two types of syllables generalising the work of Piṅgala, prastāras of permutations with repetitions generalising the work of Śārṅgadeva on svara-prastāra
239/N
Nārāyaṇa Paṇḍita also generalized prastāras of combinations which were considered earlier by Varāhamihira (c. 550 AD) and Bhaṭṭotpala (c. 950 AD)
Nārāyaṇa Paṇḍita also generalized prastāras of combinations which were considered earlier by Varāhamihira (c. 550 AD) and Bhaṭṭotpala (c. 950 AD)
240/N
Nārāyaṇa Paṇḍita presents a brilliant generalization of the mātrā-vritta, which we will analyze in some depth here
Nārāyaṇa Paṇḍita presents a brilliant generalization of the mātrā-vritta, which we will analyze in some depth here
241/N
Nārāyaṇa extended earlier methods by allowing elements beyond binary values (L and G), introducing sequences with values 1, 2, …, q.
Nārāyaṇa extended earlier methods by allowing elements beyond binary values (L and G), introducing sequences with values 1, 2, …, q.
242/N
Instead of using laghus and gurus, Nārāyaa considers sequences of variable length p formed from the digits 1, 2,.. . q where q is the highest or the last digit, such that their total value or sum n is fixed.
Instead of using laghus and gurus, Nārāyaa considers sequences of variable length p formed from the digits 1, 2,.. . q where q is the highest or the last digit, such that their total value or sum n is fixed.
243/N
To explore the different patterns in the generalized mātrā-vritta-prastāra, Nārāyana introduces a range of sequences and tabular structures at the beginning of his chapter on combinatorics
To explore the different patterns in the generalized mātrā-vritta-prastāra, Nārāyana introduces a range of sequences and tabular structures at the beginning of his chapter on combinatorics
244/N
One of the most important sequences he describes is the sāmāsikī-pankti (additive sequence), which generalizes the Virahāṅka-Hemachandra sequence.
One of the most important sequences he describes is the sāmāsikī-pankti (additive sequence), which generalizes the Virahāṅka-Hemachandra sequence.
245/N
It plays a key role in calculating the saṅkhyā, or the total number of rows, in the prasthāra. In verses 13–14 of the Ankapaśa chapter of Gaitakaumudī, Nārāyana defines the sāmāsikī-pankti in detail. x.com
It plays a key role in calculating the saṅkhyā, or the total number of rows, in the prasthāra. In verses 13–14 of the Ankapaśa chapter of Gaitakaumudī, Nārāyana defines the sāmāsikī-pankti in detail. x.com
248/N
So, Nārāyaṇa Paṇḍita provided a method to generate a general purpose sequence for which Virahāṅka-Hemachandra sequence (later known as Fibonacci sequence) becomes a special case
So, Nārāyaṇa Paṇḍita provided a method to generate a general purpose sequence for which Virahāṅka-Hemachandra sequence (later known as Fibonacci sequence) becomes a special case
250/N
Chhanda Shastra (छन्द शास्त्र) - the ancient Indian study of prosody - reveals groundbreaking concepts, including binary representation, combinatorics, Pascal’s Triangle, and the Fibonacci sequence, developed in India at least 2000 years before their emergence in Europe
Chhanda Shastra (छन्द शास्त्र) - the ancient Indian study of prosody - reveals groundbreaking concepts, including binary representation, combinatorics, Pascal’s Triangle, and the Fibonacci sequence, developed in India at least 2000 years before their emergence in Europe
251/N
Chhanda Shastra is not just the heartbeat of Sanskrit poetry - it is a testament to the mathematical and philosophical genius of ancient India. Through patterns of sound and rhythm, it encodes truths that transcend language, bridging art and computation.
Chhanda Shastra is not just the heartbeat of Sanskrit poetry - it is a testament to the mathematical and philosophical genius of ancient India. Through patterns of sound and rhythm, it encodes truths that transcend language, bridging art and computation.
252/N
From combinatorics to recursion, the echoes of Chhanda resonate through modern mathematics and computer science, reminding us that algorithms once flowed from verses, and elegance was measured in syllables.
From combinatorics to recursion, the echoes of Chhanda resonate through modern mathematics and computer science, reminding us that algorithms once flowed from verses, and elegance was measured in syllables.
253/N
The genius of Chhanda lies in how ancient Indian scholars fused the realms of music, linguistics, and computation into a single, harmonious framework - transforming patterns of sound into algorithms and verses into mathematical blueprints.
The genius of Chhanda lies in how ancient Indian scholars fused the realms of music, linguistics, and computation into a single, harmonious framework - transforming patterns of sound into algorithms and verses into mathematical blueprints.
254/N
May we continue to uncover and honor the depth of this ancient Indian legacy - where poetry met precision, and imagination shaped infinity.
May we continue to uncover and honor the depth of this ancient Indian legacy - where poetry met precision, and imagination shaped infinity.
Loading suggestions...