1/N
This is a thread on how ancient Indians pioneered the field of large numbers & fast-growing functions - what is today known as Googology.
This is a thread on how ancient Indians pioneered the field of large numbers & fast-growing functions - what is today known as Googology.
2/N
For our journey into ancient Indiaās discovery of large numbers, we will look into multiple schools of thoughts including Vedic, Jaina & Buddhist.
For our journey into ancient Indiaās discovery of large numbers, we will look into multiple schools of thoughts including Vedic, Jaina & Buddhist.
3/N
Before we delve into the topics, itās important to talk a bit more about the scope of the topic.
Before we delve into the topics, itās important to talk a bit more about the scope of the topic.
4/N
Disclaimer 1: The extent of work available on the topic of large numbers from ancient Indian literature is vast. I will only address a fairly limited aspect of the foundation of large numbers in this thread.
Disclaimer 1: The extent of work available on the topic of large numbers from ancient Indian literature is vast. I will only address a fairly limited aspect of the foundation of large numbers in this thread.
5/N
Disclaimer 2: The ancient Indians delved deeply into the notion of infinity as well. While this is very related to the concept of large numbers, infinity in the Indic context is a separate topic by itself. So I will not talk about infinity in this thread.
Disclaimer 2: The ancient Indians delved deeply into the notion of infinity as well. While this is very related to the concept of large numbers, infinity in the Indic context is a separate topic by itself. So I will not talk about infinity in this thread.
6/N
Disclaimer 3: To keep the material accessible, I have avoided use of modern googological notations such as āKnuthās up-arrow notationā, āConway chained arrow notationā etc in representing the large numbers
Disclaimer 3: To keep the material accessible, I have avoided use of modern googological notations such as āKnuthās up-arrow notationā, āConway chained arrow notationā etc in representing the large numbers
7/N
With the above important disclaimers out of the way, we are now ready for the main topic.
With the above important disclaimers out of the way, we are now ready for the main topic.
8/N
First we will look into the application of large numbers in Vedas. But before we do that, we will take a brief detour and try to understand the role of large numbers in the context of Vedic rituals.
First we will look into the application of large numbers in Vedas. But before we do that, we will take a brief detour and try to understand the role of large numbers in the context of Vedic rituals.
9/N
Yajna (ą¤Æą¤ą„ą¤) or fire based ritual is a very important aspect of Vedic way of life where the primary goal is self-realization
Yajna (ą¤Æą¤ą„ą¤) or fire based ritual is a very important aspect of Vedic way of life where the primary goal is self-realization
10/N
Yajna (ą¤Æą¤ą„ą¤) in its essence represents any action or work done, inner or outer, with an attitude of surrender and offering to the superconsciousness (ą¤¬ą„ą¤°ą¤¹ą„ą¤®ą¤Øą„) - embodiment of Truth (ą¤ą¤¤ą¤®ą„)
Yajna (ą¤Æą¤ą„ą¤) in its essence represents any action or work done, inner or outer, with an attitude of surrender and offering to the superconsciousness (ą¤¬ą„ą¤°ą¤¹ą„ą¤®ą¤Øą„) - embodiment of Truth (ą¤ą¤¤ą¤®ą„)
11/N
Yajman (ą¤Æą¤ą¤®ą¤¾ą¤Ø) in this context is the individual whose aspiration is to go through the transformative process of self-realization
Yajman (ą¤Æą¤ą¤®ą¤¾ą¤Ø) in this context is the individual whose aspiration is to go through the transformative process of self-realization
12/N
One of the primary offerings made to fire in Yajna is Ghrita (ą¤ą„ą¤¤) or clarified butter. Ghrta in this context symbolizes an illumined mind, purified with the light of intuition, golden in hue.
One of the primary offerings made to fire in Yajna is Ghrita (ą¤ą„ą¤¤) or clarified butter. Ghrta in this context symbolizes an illumined mind, purified with the light of intuition, golden in hue.
13/N
Agni (ą¤ ą¤ą„ą¤Øą¤æ) is fire, the ultimate transformative agent. It symbolizes the divine Will that takes up the action in all consecration of works. Agni is a flame of force instinct with the light of divine knowledge. Agni is the seer-will in the universe unerring in all its works
Agni (ą¤ ą¤ą„ą¤Øą¤æ) is fire, the ultimate transformative agent. It symbolizes the divine Will that takes up the action in all consecration of works. Agni is a flame of force instinct with the light of divine knowledge. Agni is the seer-will in the universe unerring in all its works
14/N
The ground where this fire ritual is done is called Vedi (ą¤µą„ą¤¦ą„). It represents an individual with such a mind whose foundation has been prepared with pre-requisite knowledge of self realization (ą¤µą¤æą¤¦ą„ą¤Æą¤¾)
The ground where this fire ritual is done is called Vedi (ą¤µą„ą¤¦ą„). It represents an individual with such a mind whose foundation has been prepared with pre-requisite knowledge of self realization (ą¤µą¤æą¤¦ą„ą¤Æą¤¾)
15/N
The Shulba Sutras provide detailed instructions for how to perform Yajna or fire based rituals including construction of the ą¤ą¤æą¤¤ą¤æ (Chiti) or altar - which requires detailed understanding of structural engineering in three dimensions.
The Shulba Sutras provide detailed instructions for how to perform Yajna or fire based rituals including construction of the ą¤ą¤æą¤¤ą¤æ (Chiti) or altar - which requires detailed understanding of structural engineering in three dimensions.
16/N
Chiti (ą¤ą¤æą¤¤ą¤æ) represents the core of consciousness (ą¤ą¤æą¤¤ą„ą¤¤ / Chitta) where the transformation from all layers of the being takes place with the help of Agni.
Chiti (ą¤ą¤æą¤¤ą¤æ) represents the core of consciousness (ą¤ą¤æą¤¤ą„ą¤¤ / Chitta) where the transformation from all layers of the being takes place with the help of Agni.
17/N
The construction of the altar requires careful selection of different sizes of bricks called ą¤ą¤·ą„ą¤ą¤ą¤¾ (Ishtaka) in Sanskrit. These bricks need to carefully used to satisfy a set of geometrical constraints to form the 3D altar
The construction of the altar requires careful selection of different sizes of bricks called ą¤ą¤·ą„ą¤ą¤ą¤¾ (Ishtaka) in Sanskrit. These bricks need to carefully used to satisfy a set of geometrical constraints to form the 3D altar
18/N
These ą¤ą¤·ą„ą¤ą¤ą¤¾ or bricks represent the great resolution & will power of the individual (ą¤Æą¤ą¤®ą¤¾ą¤Ø) who is willing to sacrifice those aspects of her being where the light of consciousness has not reached yet
These ą¤ą¤·ą„ą¤ą¤ą¤¾ or bricks represent the great resolution & will power of the individual (ą¤Æą¤ą¤®ą¤¾ą¤Ø) who is willing to sacrifice those aspects of her being where the light of consciousness has not reached yet
19/N
The end-products of the Yajna are Gau (cows) & Ashva (horses) which represent two companion ideas of Light (ą¤ą„) and Energy (ą¤ ą¤¶ą„ą¤µ) - the twin aspect of all the activities of existence. They are symbolic of the richness of mental illumination & abundance of pure vital energy.
The end-products of the Yajna are Gau (cows) & Ashva (horses) which represent two companion ideas of Light (ą¤ą„) and Energy (ą¤ ą¤¶ą„ą¤µ) - the twin aspect of all the activities of existence. They are symbolic of the richness of mental illumination & abundance of pure vital energy.
20/N
Now, we are ready to see why large numbers were used in Vedic rituals.
Now, we are ready to see why large numbers were used in Vedic rituals.
21/N
In Shukla Yajurveda 17.2, we find a Mantra where the individual who is an aspirant of self-realization is wishing how both the material of the Yajna and the ultimate fruit in abundance would help in his transformative journey.
In Shukla Yajurveda 17.2, we find a Mantra where the individual who is an aspirant of self-realization is wishing how both the material of the Yajna and the ultimate fruit in abundance would help in his transformative journey.
22/N
Notice, how large numbers have been used to āquantifyā mental & vital abundance. Below I am providing a rough translation of Shukla Yajurveda 17.2
Notice, how large numbers have been used to āquantifyā mental & vital abundance. Below I am providing a rough translation of Shukla Yajurveda 17.2
23/N
Translation of Shukla Yajurveda 17.2 is given below
Translation of Shukla Yajurveda 17.2 is given below
24/N
Notice how the numbers have been named in the Shukla Yajurveda 17.2 Mantra: starting from Eka (one) to Parardha (10^18 - ten raised to the power of 18). I am summarizing the large numbers mentioned in Yajurveda here
Notice how the numbers have been named in the Shukla Yajurveda 17.2 Mantra: starting from Eka (one) to Parardha (10^18 - ten raised to the power of 18). I am summarizing the large numbers mentioned in Yajurveda here
25/N
The Vedas are so ancient that they are hard to date. Traditionally they are considered āApaurusheya'' or texts that are revealed to self-realized Rishis
The Vedas are so ancient that they are hard to date. Traditionally they are considered āApaurusheya'' or texts that are revealed to self-realized Rishis
26/N
According to some researchers archeo-astronomy evidence exists to show that the earliest Vedic hymns were written before 22,000 BCE !
According to some researchers archeo-astronomy evidence exists to show that the earliest Vedic hymns were written before 22,000 BCE !
27/N
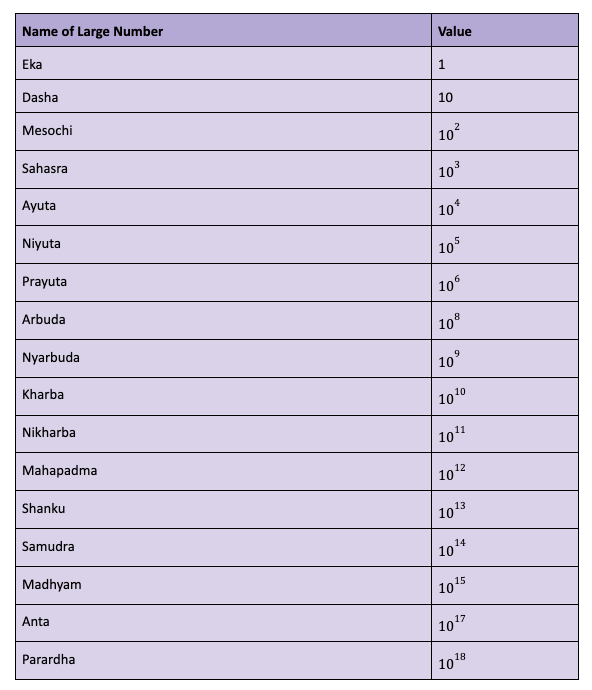
It is simply mind-boggling to think that numbers as large as Parardha (10^18) were known to ancient Indians possibly by 22,000 BCE
It is simply mind-boggling to think that numbers as large as Parardha (10^18) were known to ancient Indians possibly by 22,000 BCE
28/N
Now, we are going to look at the great Indian epic Ramayana to continue our journey of large numbers
Now, we are going to look at the great Indian epic Ramayana to continue our journey of large numbers
29/N
In Ramayana Yuddha Kanda, we find ą¤¶ą„ą¤ (Shuka), one of the administrative chiefs of the mighty & scholarly King Ravana, was commissioned to collect information about the army of Bhagavan Ramachandra, an Avatara and the magnificent prince of Ayodhya from Ikshvaku dynasty.
In Ramayana Yuddha Kanda, we find ą¤¶ą„ą¤ (Shuka), one of the administrative chiefs of the mighty & scholarly King Ravana, was commissioned to collect information about the army of Bhagavan Ramachandra, an Avatara and the magnificent prince of Ayodhya from Ikshvaku dynasty.
30/N
In this context, ą¤¶ą„ą¤ gives a description of large numbers. He says āIt is said by wise men that hundred thousand crores multiplied by hundred thousand crores as referred to as Shankuā
In this context, ą¤¶ą„ą¤ gives a description of large numbers. He says āIt is said by wise men that hundred thousand crores multiplied by hundred thousand crores as referred to as Shankuā
31/N
Shanku as described in Ramayana is one trillion - 10 raised to the power of 12 or 10^12
Shanku as described in Ramayana is one trillion - 10 raised to the power of 12 or 10^12
32/N
Shuka (ą¤¶ą„ą¤) in Ramayana then continues to define even larger numbers. He uses Shatam Sahasram & Shanku as the basis to describe increasingly larger numbers. Here we see the early application of building large numbers using a fast growing function
Shuka (ą¤¶ą„ą¤) in Ramayana then continues to define even larger numbers. He uses Shatam Sahasram & Shanku as the basis to describe increasingly larger numbers. Here we see the early application of building large numbers using a fast growing function
33/N
In this case, we see Shuka in Ramayana building up to the number Maha Augha, which is 10 raised to the power of 60 (10^60)
In this case, we see Shuka in Ramayana building up to the number Maha Augha, which is 10 raised to the power of 60 (10^60)
34/N
I am summarizing Shukaās description from Ramayana in a tabular format below
I am summarizing Shukaās description from Ramayana in a tabular format below
35/N
Ravanaās minister Shuka then sums up the unimaginable strength of Ramaās army of Vaanara sena in a very quantifiable manner.
Ravanaās minister Shuka then sums up the unimaginable strength of Ramaās army of Vaanara sena in a very quantifiable manner.
36/N
So, from Shukaās description, we can assess that the equivalent strength of Ramaās army can be computed as given below. Notice that Shuka is talking about the effective strength of the army - not the number of soldiers.
So, from Shukaās description, we can assess that the equivalent strength of Ramaās army can be computed as given below. Notice that Shuka is talking about the effective strength of the army - not the number of soldiers.
38/N
Dr. P V Vartak proposed 4 December 7324 BCE as the day of Rama-Janma. Nilesh Oak gives a date of 12200 BCE primarily based on archeo-astronomy.
Dr. P V Vartak proposed 4 December 7324 BCE as the day of Rama-Janma. Nilesh Oak gives a date of 12200 BCE primarily based on archeo-astronomy.
39/N
Essentially very large numbers such as Maha Augha (10^60) were already in common parlance by at least 7400 BCE in India.
Essentially very large numbers such as Maha Augha (10^60) were already in common parlance by at least 7400 BCE in India.
40/N
Next we will focus on Jaina literature to understand the concept of Vargita-samvargita: a process to generate very large numbers using an iterative method.
Next we will focus on Jaina literature to understand the concept of Vargita-samvargita: a process to generate very large numbers using an iterative method.
41/N
A detailed description of Vargita-samvargita is found in the į¹¢aį¹khandagama, which is the foremost and oldest Digambara Jain sacred text. į¹¢aį¹khandagama is dated to be compiled no later than 200 CE
A detailed description of Vargita-samvargita is found in the į¹¢aį¹khandagama, which is the foremost and oldest Digambara Jain sacred text. į¹¢aį¹khandagama is dated to be compiled no later than 200 CE
42/N
Acharya Virasena was a brilliant mathematician. He was also proficient in astronomy, grammar, logic, mathematics and prosody.
Acharya Virasena was a brilliant mathematician. He was also proficient in astronomy, grammar, logic, mathematics and prosody.
43/N
Virasena wrote a 72,000 shloka commentary on Shatkhandagama (known as Dhavala and the last section called Mahadhavala). Dhavala is dated to be composed no later than 9th century CE
Virasena wrote a 72,000 shloka commentary on Shatkhandagama (known as Dhavala and the last section called Mahadhavala). Dhavala is dated to be composed no later than 9th century CE
44/N
Virasena mentions the process of Vargita-samvargita in Dhavala Part 3
Virasena mentions the process of Vargita-samvargita in Dhavala Part 3
45/N
A description of the Vargita-samvargita process using modern notation is provided below
A description of the Vargita-samvargita process using modern notation is provided below
46/N
Before we delve into specific large numbers in Jaina mathematics, letās do a quick survey of the ontology of the number system itself from a Jaina perspective.
Before we delve into specific large numbers in Jaina mathematics, letās do a quick survey of the ontology of the number system itself from a Jaina perspective.
47/N
We are going to refer to the brilliant Jain text Anuyogadwara Sutra dated no later than 100 BCE.
We are going to refer to the brilliant Jain text Anuyogadwara Sutra dated no later than 100 BCE.
48/N
Ganana Samkhya (samkhya as counting) is as follows
1. Samkhyat (countable)
2. Asamkhyat (innumerable)
3. Anant (infinite)
Ganana Samkhya (samkhya as counting) is as follows
1. Samkhyat (countable)
2. Asamkhyat (innumerable)
3. Anant (infinite)
49/N
Samkhyat (countable) is of three kinds
1. Jaghanya Samkhyat (countable min)
2. Utkrishta Samkhyat (countable max)
3. Ajaghanya-Anutkrisht Samkhyat (countable intermediate)
Samkhyat (countable) is of three kinds
1. Jaghanya Samkhyat (countable min)
2. Utkrishta Samkhyat (countable max)
3. Ajaghanya-Anutkrisht Samkhyat (countable intermediate)
50/N
Asamkhyat (innumerable) is of three kinds
1. Parit Asamkhyat (lower innumerable)
2. Yukta Asamkhyat (innumerable raised to the power of itself)
3. Asamkhyat Asamkhyat (innumerable-innumerable)
Asamkhyat (innumerable) is of three kinds
1. Parit Asamkhyat (lower innumerable)
2. Yukta Asamkhyat (innumerable raised to the power of itself)
3. Asamkhyat Asamkhyat (innumerable-innumerable)
51/N
Parit Asamkhyat (lower innumerable) is of three kinds
1. Jaghanya Parit Asamkhyat (minimum lower innumerable)
2. Utkrisht Parit Asamkhyat (maximum lower innumerable)
3. Ajaghanyaauthkrish Parit Asamkhyat (intermediate lower innumerable)
Parit Asamkhyat (lower innumerable) is of three kinds
1. Jaghanya Parit Asamkhyat (minimum lower innumerable)
2. Utkrisht Parit Asamkhyat (maximum lower innumerable)
3. Ajaghanyaauthkrish Parit Asamkhyat (intermediate lower innumerable)
52/N
Yukta Asamkhyat is of 3 kinds
1. Jaghanya Yukt Asamkhyat (innumerable raised to the power of itself, min)
2. Utkrisht Yukt Asamkhyat (innumerable raised to the power of itself, max)
3. Ajaghanya-Anutkrisht Yukt Asamkhyat (innumerable raised to power of itself, intermediate)
Yukta Asamkhyat is of 3 kinds
1. Jaghanya Yukt Asamkhyat (innumerable raised to the power of itself, min)
2. Utkrisht Yukt Asamkhyat (innumerable raised to the power of itself, max)
3. Ajaghanya-Anutkrisht Yukt Asamkhyat (innumerable raised to power of itself, intermediate)
53/N
Asamkhyat-Asamkhyat is of 3 kinds
1. Jaghanya Asamkhyat-Asamkhyat (min innumerable-innumerable)
2. Utkrisht Asamkhyat-Asamkhyat (max innumerable-innumerable)
3. Ajaghanya-Anutkrisht Asamkhyat-Asamkhyat (intermediate innumerable-innumerable)
Asamkhyat-Asamkhyat is of 3 kinds
1. Jaghanya Asamkhyat-Asamkhyat (min innumerable-innumerable)
2. Utkrisht Asamkhyat-Asamkhyat (max innumerable-innumerable)
3. Ajaghanya-Anutkrisht Asamkhyat-Asamkhyat (intermediate innumerable-innumerable)
54/N
Ananta (infinite) is of three kinds:
1. Parit Ananta (lower infinite)
2. Yukt Ananta (infinite raised to power of itself)
3. Ananta Ananta (infinite-infinite)
Ananta (infinite) is of three kinds:
1. Parit Ananta (lower infinite)
2. Yukt Ananta (infinite raised to power of itself)
3. Ananta Ananta (infinite-infinite)
55/N
Parit Ananta is of three kinds
1. Jaghanya Parit Ananta (min lower infinite)
2. Utkrisht Parit Ananta (max lower infinite)
3. Ajaghanya-Anutkrisht Parit Ananta (intermediate lower infinite)
Parit Ananta is of three kinds
1. Jaghanya Parit Ananta (min lower infinite)
2. Utkrisht Parit Ananta (max lower infinite)
3. Ajaghanya-Anutkrisht Parit Ananta (intermediate lower infinite)
56/N
Yukta Ananta is of three kinds
1. Jaghanya Yukta Ananta (min lower infinite)
2. Utkrisht Yukta Ananta (max lower infinite)
3. Ajaghanya-Anutkrisht Yukta Ananta (intermediate lower infinite)
Yukta Ananta is of three kinds
1. Jaghanya Yukta Ananta (min lower infinite)
2. Utkrisht Yukta Ananta (max lower infinite)
3. Ajaghanya-Anutkrisht Yukta Ananta (intermediate lower infinite)
57/N
Ananta Ananta is of three kinds
1. Jaghanya Ananta Ananta (min infinite infinite)
2. Utkrisht Ananta Ananta (max infinite infinite)
3. Ajaghanya-Anutkrisht Ananta Ananta (intermediate infinite infinite)
Ananta Ananta is of three kinds
1. Jaghanya Ananta Ananta (min infinite infinite)
2. Utkrisht Ananta Ananta (max infinite infinite)
3. Ajaghanya-Anutkrisht Ananta Ananta (intermediate infinite infinite)
58/N
We are going to focus on the number Jaghanya Parita Asaį¹khyata which is the smallest nearly innumerable number and the largest numerable number.
We are going to focus on the number Jaghanya Parita Asaį¹khyata which is the smallest nearly innumerable number and the largest numerable number.
59/N
There is a precise definition for the number Jaghanya Parita Asaį¹khyata. To understand that we need to have a primer on Jaina cosmology.
There is a precise definition for the number Jaghanya Parita Asaį¹khyata. To understand that we need to have a primer on Jaina cosmology.
60/N
According to Jain cosmology, Jambudweepa (Jambu island) is at the center of Madhyaloka, or the middle part of the universe
According to Jain cosmology, Jambudweepa (Jambu island) is at the center of Madhyaloka, or the middle part of the universe
61/N
JambÅ«dvÄ«paprajƱapti contains a description of JambÅ«dvÄ«pa and life biographies of Rishabha and King Bharata.
JambÅ«dvÄ«paprajƱapti contains a description of JambÅ«dvÄ«pa and life biographies of Rishabha and King Bharata.
62/N
TrilokasÄra, TrilokaprajƱapti, TrilokadipikÄ and Kį¹£etrasamÄsa are the other texts that provide the details of JambÅ«dvÄ«pa and Jaina cosmology.
TrilokasÄra, TrilokaprajƱapti, TrilokadipikÄ and Kį¹£etrasamÄsa are the other texts that provide the details of JambÅ«dvÄ«pa and Jaina cosmology.
63/N
The middle world consists of a central island, which is surrounded by alternating annular oceans and islands.
The middle world consists of a central island, which is surrounded by alternating annular oceans and islands.
64/N
The central circular island called JambudwÄ«pa is surrounded by an annular ocean called Lavaį¹a Ocean.
The central circular island called JambudwÄ«pa is surrounded by an annular ocean called Lavaį¹a Ocean.
65/N
An annular island called DhÄtakÄ«khaį¹įøa surrounds the Lavaį¹a Ocean.
An annular island called DhÄtakÄ«khaį¹įøa surrounds the Lavaį¹a Ocean.
66/N
DhÄtakÄ«khaį¹įøa is surrounded by an annular ocean called KÄlodadhi, which is again surrounded by an island called Puį¹£karavara.
DhÄtakÄ«khaį¹įøa is surrounded by an annular ocean called KÄlodadhi, which is again surrounded by an island called Puį¹£karavara.
67/N
This pattern continues till the edge of the universe. The number of these concentric islands and oceans is extremely large.
This pattern continues till the edge of the universe. The number of these concentric islands and oceans is extremely large.
68/N
The definition of jaghanya-parita-asamkhyata is linked to this cosmology. First we setup the problem with formal notation with the help of a diagram
The definition of jaghanya-parita-asamkhyata is linked to this cosmology. First we setup the problem with formal notation with the help of a diagram
69/N
Formal definition of the googlogical number Jaghanya Parita Asaį¹khyata is given here
Formal definition of the googlogical number Jaghanya Parita Asaį¹khyata is given here
70/N
Finally the formal definition of Jaghanya Parita Asaį¹khyata is given here
Finally the formal definition of Jaghanya Parita Asaį¹khyata is given here
71/N
Here we show how to find the value of n_0
Here we show how to find the value of n_0
72/N
Analysis of how to find the value of n_0 continues here
Analysis of how to find the value of n_0 continues here
73/N
Here it is shown how to find the value of n_0 as found in Trilokasara
Here it is shown how to find the value of n_0 as found in Trilokasara
74/N
Trilokasara Gatha 17
Trilokasara Gatha 17
75/N
Trilokasara Gatha 18
Trilokasara Gatha 18
76/N
Trilokasara Gatha 21
Trilokasara Gatha 21
77/N
Trilokasara Gatha 22
Trilokasara Gatha 22
78/N
Trilokasara Gatha 28
(Note the value here. This is what we derived earlier)
Trilokasara Gatha 28
(Note the value here. This is what we derived earlier)
79/N
It is important to note that the rules in Trilokasara gatha 22 and Trilokasara gatha 23 are very similar to what was already given by Brahmagupta in his Brahmasphuta-Siddhanta which was composed earlier than Trilokasara gatha
It is important to note that the rules in Trilokasara gatha 22 and Trilokasara gatha 23 are very similar to what was already given by Brahmagupta in his Brahmasphuta-Siddhanta which was composed earlier than Trilokasara gatha
80/N
There is a very interesting and intricate counting mechanism which leads to the unfathomably large number jaghanya-parita-asamkhyata
There is a very interesting and intricate counting mechanism which leads to the unfathomably large number jaghanya-parita-asamkhyata
81/N
The description of the iterative counting method to find jaghanya-parita-asamkhyata
continues
The description of the iterative counting method to find jaghanya-parita-asamkhyata
continues
82/N
As will be seen below, the number jaghanya-parita-asamkhyata is very large. We will find a tight lower bound for its value.
As will be seen below, the number jaghanya-parita-asamkhyata is very large. We will find a tight lower bound for its value.
83/N
However, before we can find a lower value, we need to find a recursive relation between n_(i+1) and n_(i) using the principle of vargita-samvargita discussed earlier.
However, before we can find a lower value, we need to find a recursive relation between n_(i+1) and n_(i) using the principle of vargita-samvargita discussed earlier.
84/N
Here we find a general expression of n and r first
Here we find a general expression of n and r first
85/N
Here we find a cool relationship between n_(i+1) and n_(i) using the principle of vargita-samvargita - which will come handy next to find a lower bound of jaghanya-parita-asamkhyata
Here we find a cool relationship between n_(i+1) and n_(i) using the principle of vargita-samvargita - which will come handy next to find a lower bound of jaghanya-parita-asamkhyata
86/N
Finally, we are ready to assess a lower-bound of the humongous number jaghanya-parita-asamkhyata.
Finally, we are ready to assess a lower-bound of the humongous number jaghanya-parita-asamkhyata.
87/N
Now we will discuss the large numbers in Lalitavistara SÅ«tra, a prominent Buddhist text (no later than 300 CE)
Now we will discuss the large numbers in Lalitavistara SÅ«tra, a prominent Buddhist text (no later than 300 CE)
88/N
The Lalitavistara SÅ«tra is a Sanskrit Mahayana Buddhist sutra that tells the story of Gautama Buddha from the time of his descent from Tushita until his first sermon at Sarnath near Varanasi.
The Lalitavistara SÅ«tra is a Sanskrit Mahayana Buddhist sutra that tells the story of Gautama Buddha from the time of his descent from Tushita until his first sermon at Sarnath near Varanasi.
89/N
In the 12th chapter of Lalitavistara Sutra (ą¤¶ą¤æą¤²ą„ą¤Ŗą¤øą¤ą¤¦ą¤°ą„ą¤¶ą¤Øą¤Ŗą¤°ą¤æą¤µą¤°ą„ą¤¤ą¤), we find that grand preparation for selecting a bridegroom for the Prince Sarvarthasiddha (Buddha) was ongoing in Kapilavastu.
In the 12th chapter of Lalitavistara Sutra (ą¤¶ą¤æą¤²ą„ą¤Ŗą¤øą¤ą¤¦ą¤°ą„ą¤¶ą¤Øą¤Ŗą¤°ą¤æą¤µą¤°ą„ą¤¤ą¤), we find that grand preparation for selecting a bridegroom for the Prince Sarvarthasiddha (Buddha) was ongoing in Kapilavastu.
90/N
Here is the reference from 12th chapter of Lalitavistara Sutra
Here is the reference from 12th chapter of Lalitavistara Sutra
91/N
The reference from 12th chapter of Lalitavistara Sutra continues here
The reference from 12th chapter of Lalitavistara Sutra continues here
92/N
Prince Sarvarthasiddha (Buddha) did not want a regular princess to marry.
Prince Sarvarthasiddha (Buddha) did not want a regular princess to marry.
93/N
The prince wrote a collection of verses describing the desired qualities of the bride which included: knowledge of the Dharma, nobility of thoughts, elegance of appearance, prosperity of mind, expertise in public administration & public speech.
The prince wrote a collection of verses describing the desired qualities of the bride which included: knowledge of the Dharma, nobility of thoughts, elegance of appearance, prosperity of mind, expertise in public administration & public speech.
94/N
Gopa, daughter of Dandapani, from Kapilavastu was exquisitely beautiful & wise. She had all the qualities Sarvarthasiddha was looking for.
Gopa, daughter of Dandapani, from Kapilavastu was exquisitely beautiful & wise. She had all the qualities Sarvarthasiddha was looking for.
95/N
Shudhhodana, father of Sarvarthasiddha sent the marriage proposal for Gopa and his son to Dandapani, father of the future bride.
Shudhhodana, father of Sarvarthasiddha sent the marriage proposal for Gopa and his son to Dandapani, father of the future bride.
96/N
However Dandapani sent a message back saying āWe have a family custom not to have our daughter married to someone who is not an expert in art such as swordsmanship, wrestling and topics of science such as mathematics & astronomyā
However Dandapani sent a message back saying āWe have a family custom not to have our daughter married to someone who is not an expert in art such as swordsmanship, wrestling and topics of science such as mathematics & astronomyā
97/N
Given this condition from the brideās family, a grand event was held, where five hundred Shakya princes were invited in a competition where prince Sarvarthasiddha could compete & demonstrate his expertise on topics of art and science.
Given this condition from the brideās family, a grand event was held, where five hundred Shakya princes were invited in a competition where prince Sarvarthasiddha could compete & demonstrate his expertise on topics of art and science.
98/N
In that grand competition, Sarvarthasiddha had to compete with a brilliant mathematician from Kapilavastu named Arjuna.
In that grand competition, Sarvarthasiddha had to compete with a brilliant mathematician from Kapilavastu named Arjuna.
99/N
Arjuna asked Sarvarthasiddha, āDo you, Prince, know the order of reckoning after a Koti Shata (10 raised to the power of 9)ā ?
Arjuna asked Sarvarthasiddha, āDo you, Prince, know the order of reckoning after a Koti Shata (10 raised to the power of 9)ā ?
110/N
Sarvarthasiddha showed off his skills in mathematics by citing the names of the powers of ten, up to āTallakshanaā, which equals to 10 raised to the power of 53.
Sarvarthasiddha showed off his skills in mathematics by citing the names of the powers of ten, up to āTallakshanaā, which equals to 10 raised to the power of 53.
101/N
Because the list of large numbers as mentioned in Lalitavistara SÅ«tra is pretty long, I have broken it up in parts. In the first part, Sarvarthasiddha (Buddha) goes from Ayuta (10 raised to the power of 9) to Hetuhila (10 raised to the power of 31)
Because the list of large numbers as mentioned in Lalitavistara SÅ«tra is pretty long, I have broken it up in parts. In the first part, Sarvarthasiddha (Buddha) goes from Ayuta (10 raised to the power of 9) to Hetuhila (10 raised to the power of 31)
102/N
Here Sarvarthasiddha (Buddha) goes from Karahu (10 raised to the power of 33) to Tallakshana (10 raised to the power of 53)
Here Sarvarthasiddha (Buddha) goes from Karahu (10 raised to the power of 33) to Tallakshana (10 raised to the power of 53)
103/N
But Sarvarthasiddha did not stop there. He then explained how this series can be extended geometrically.
But Sarvarthasiddha did not stop there. He then explained how this series can be extended geometrically.
104/N
He starts from Dhvajagravati (10 raised to the power of 99). The last number at which he arrived at after going through seven successive steps was Paramanurajahpravesha (ą¤Ŗą¤°ą¤®ą¤¾ą¤Øą„ą¤°ą¤ą¤ą¤Ŗą„ą¤°ą¤µą„ą¤¶), which is 10 raised to the power of 421
He starts from Dhvajagravati (10 raised to the power of 99). The last number at which he arrived at after going through seven successive steps was Paramanurajahpravesha (ą¤Ŗą¤°ą¤®ą¤¾ą¤Øą„ą¤°ą¤ą¤ą¤Ŗą„ą¤°ą¤µą„ą¤¶), which is 10 raised to the power of 421
105/N
Below I am providing the rest of the table as mentioned in Lalitavistara Sutra
Below I am providing the rest of the table as mentioned in Lalitavistara Sutra
106/N
The very large ntity ą¤Ŗą¤°ą¤®ą¤¾ą¤Øą„ą¤°ą¤ą¤ą¤Ŗą„ą¤°ą¤µą„ą¤¶ (10 ^ 421) has been compared with the conceptual vastness of Tathagata Bodhisattva.
The very large ntity ą¤Ŗą¤°ą¤®ą¤¾ą¤Øą„ą¤°ą¤ą¤ą¤Ŗą„ą¤°ą¤µą„ą¤¶ (10 ^ 421) has been compared with the conceptual vastness of Tathagata Bodhisattva.
107/N
Next we we will to BuddhÄvataį¹saka SÅ«tra, an important MahÄyÄna Buddhist text for our exploration of large numbers.
Next we we will to BuddhÄvataį¹saka SÅ«tra, an important MahÄyÄna Buddhist text for our exploration of large numbers.
108/N
BuddhÄvataį¹saka SÅ«tra is one of the most influential MahÄyÄna Buddhist sutras. It is also often referred to as the Avataį¹saka SÅ«tra. In Sanskrit, the term Avataį¹saka means āa great number,ā āa multitude,ā or āa collection.ā
BuddhÄvataį¹saka SÅ«tra is one of the most influential MahÄyÄna Buddhist sutras. It is also often referred to as the Avataį¹saka SÅ«tra. In Sanskrit, the term Avataį¹saka means āa great number,ā āa multitude,ā or āa collection.ā
109/N
The original BuddhÄvataį¹saka SÅ«tra was in Sanskrit, which was later translated to Tibetan & Chinese
The original BuddhÄvataį¹saka SÅ«tra was in Sanskrit, which was later translated to Tibetan & Chinese
110/N
According to Akira Hirakawa and Otake Susumu Sanskrit original of BuddhÄvataį¹saka SÅ«tra, was compiled in India about 500 years after death of Gautama Buddha
According to Akira Hirakawa and Otake Susumu Sanskrit original of BuddhÄvataį¹saka SÅ«tra, was compiled in India about 500 years after death of Gautama Buddha
111/N
In this text we will find how Buddha provides a fast growing function. The last number in the series is a called āAnabhilapyanabhilapya -Parivartaā which is 10 raised to the power of 37,218,383,881,977,700,000,000,000,000,000,000,000
In this text we will find how Buddha provides a fast growing function. The last number in the series is a called āAnabhilapyanabhilapya -Parivartaā which is 10 raised to the power of 37,218,383,881,977,700,000,000,000,000,000,000,000
112/N
In the 30th Book of the BuddhÄvataį¹saka SÅ«tra (ą¤ ą¤øą¤ą¤ą„ą¤Æą„ą¤Æ), we find a Bodhisattva asking the Buddha: āO Bhagavat, when expounding on the Dharma, the buddhas, the tathÄgatas, use very large numbersā
In the 30th Book of the BuddhÄvataį¹saka SÅ«tra (ą¤ ą¤øą¤ą¤ą„ą¤Æą„ą¤Æ), we find a Bodhisattva asking the Buddha: āO Bhagavat, when expounding on the Dharma, the buddhas, the tathÄgatas, use very large numbersā
113/N
Bodhisattva continues: āThe tathÄgatas use such numbers as āasaį¹khyeya,ā āmeasureless,ā ābound- less,ā āincomparable,ā āinnumerable,ā āindescribable,ā āinconceivable,ā āincalculable,ā āineffable.ā O Bhagavat, what is meant by āasaį¹khyeyaā and so forth?
Bodhisattva continues: āThe tathÄgatas use such numbers as āasaį¹khyeya,ā āmeasureless,ā ābound- less,ā āincomparable,ā āinnumerable,ā āindescribable,ā āinconceivable,ā āincalculable,ā āineffable.ā O Bhagavat, what is meant by āasaį¹khyeyaā and so forth?
114/N
The Buddha then goes into this amazing discourse of listing numbers in chronological order.
The Buddha then goes into this amazing discourse of listing numbers in chronological order.
115/N
Buddha starts from Koti (10 raised to the power 7) and ends up this mind-bogglingly large umber āAnabhilapyanabhilapya-Parivartaā which is same as 10 raised to the power of 1,163,074,496,311,800,000,000,000,000,000,000,000
Buddha starts from Koti (10 raised to the power 7) and ends up this mind-bogglingly large umber āAnabhilapyanabhilapya-Parivartaā which is same as 10 raised to the power of 1,163,074,496,311,800,000,000,000,000,000,000,000
116/N
Because the list of these large numbers in BuddhÄvataį¹saka SÅ«tra is long, I will break it up into multiple tables.
Because the list of these large numbers in BuddhÄvataį¹saka SÅ«tra is long, I will break it up into multiple tables.
117/N
The following table from BuddhÄvataį¹saka SÅ«tra starts from Koti (10 raised to the power of 7) and ends with Avaga (10 raised to the power of 28672).
The following table from BuddhÄvataį¹saka SÅ«tra starts from Koti (10 raised to the power of 7) and ends with Avaga (10 raised to the power of 28672).
118/N
The next table from BuddhÄvataį¹saka SÅ«tra starts from Viturna (10 raised to the power of 7516192768) and ends with Kshamuda (10 raised to the power of 246290604621824).
The next table from BuddhÄvataį¹saka SÅ«tra starts from Viturna (10 raised to the power of 7516192768) and ends with Kshamuda (10 raised to the power of 246290604621824).
119/N
The next table from BuddhÄvataį¹saka SÅ«tra starts from Elada (10 raised to the power of 492581209243648) and ends with Hematra (10 raised to the power of 504,403,158,265,496,000).
The next table from BuddhÄvataį¹saka SÅ«tra starts from Elada (10 raised to the power of 492581209243648) and ends with Hematra (10 raised to the power of 504,403,158,265,496,000).
120/N
The next table from BuddhÄvataį¹saka SÅ«tra starts from Vematra (10 raised to the power of 1,008,806,316,530,990,000) and ends with Meruda (10 raised to the power of 16,528,282,690,043,800,000,000).
The next table from BuddhÄvataį¹saka SÅ«tra starts from Vematra (10 raised to the power of 1,008,806,316,530,990,000) and ends with Meruda (10 raised to the power of 16,528,282,690,043,800,000,000).
121/N
The next table from BuddhÄvataį¹saka SÅ«tra starts from Kheluda (10 raised to the power of 33,056,565,380,087,500,000,000) and ends with Havava (10 raised to the power of 33,849,922,949,209,600,000,000,000).
The next table from BuddhÄvataį¹saka SÅ«tra starts from Kheluda (10 raised to the power of 33,056,565,380,087,500,000,000) and ends with Havava (10 raised to the power of 33,849,922,949,209,600,000,000,000).
122/N
The next table from BuddhÄvataį¹saka SÅ«tra starts from Vivara (10 raised to the power of 67,699,845,898,419,200,000,000,000) and ends with Akshaya (10 raised to the power of 138,649,284,399,963,000,000,000,000,000)
The next table from BuddhÄvataį¹saka SÅ«tra starts from Vivara (10 raised to the power of 67,699,845,898,419,200,000,000,000) and ends with Akshaya (10 raised to the power of 138,649,284,399,963,000,000,000,000,000)
123/N
The next table from BuddhÄvataį¹saka SÅ«tra starts from Sambhuta (10 raised to the power of 277,298,568,799,925,000,000,000,000,000) and ends with Aparyanta (10 raised to the power of 1,135,814,937,804,490,000,000,000,000,000,000).
The next table from BuddhÄvataį¹saka SÅ«tra starts from Sambhuta (10 raised to the power of 277,298,568,799,925,000,000,000,000,000) and ends with Aparyanta (10 raised to the power of 1,135,814,937,804,490,000,000,000,000,000,000).
124/N
The final table from BuddhÄvataį¹saka SÅ«tra starts from Aparyanta-Parivarta (10 raised to the power of 277,298,568,799,925,000,000,000,000,000) and ends with Anabhilapyanabhilapya
-Parivarta
The final table from BuddhÄvataį¹saka SÅ«tra starts from Aparyanta-Parivarta (10 raised to the power of 277,298,568,799,925,000,000,000,000,000) and ends with Anabhilapyanabhilapya
-Parivarta
125/N
Anabhilapyanabhilapya--Parivarta
is equivalent this mind-bogglingly HUGE number (10 raised to the power of 37,218,383,881,977,700,000,000,000,000,000,000,000).
Anabhilapyanabhilapya--Parivarta
is equivalent this mind-bogglingly HUGE number (10 raised to the power of 37,218,383,881,977,700,000,000,000,000,000,000,000).
126/N
In the European context, Archimedes, a Greek polymath, sometime in the 300 BCE started experimenting with large number in his book āSand Reckonerā
In the European context, Archimedes, a Greek polymath, sometime in the 300 BCE started experimenting with large number in his book āSand Reckonerā
127/N
Ancient Indians not only pioneered the study of large numbers at least 10000 years before Greeks (or any Europeans), but were using it in both mathematical work as well as in literature and poetry.
Ancient Indians not only pioneered the study of large numbers at least 10000 years before Greeks (or any Europeans), but were using it in both mathematical work as well as in literature and poetry.
128/N
The study of large numbers invented in India is today known as googology. It is an important tool for understanding some of the fundamental principles of mathematics and for exploring the limits of what is currently known about the properties of large numbers
The study of large numbers invented in India is today known as googology. It is an important tool for understanding some of the fundamental principles of mathematics and for exploring the limits of what is currently known about the properties of large numbers
129/N
References
References
Loading suggestions...