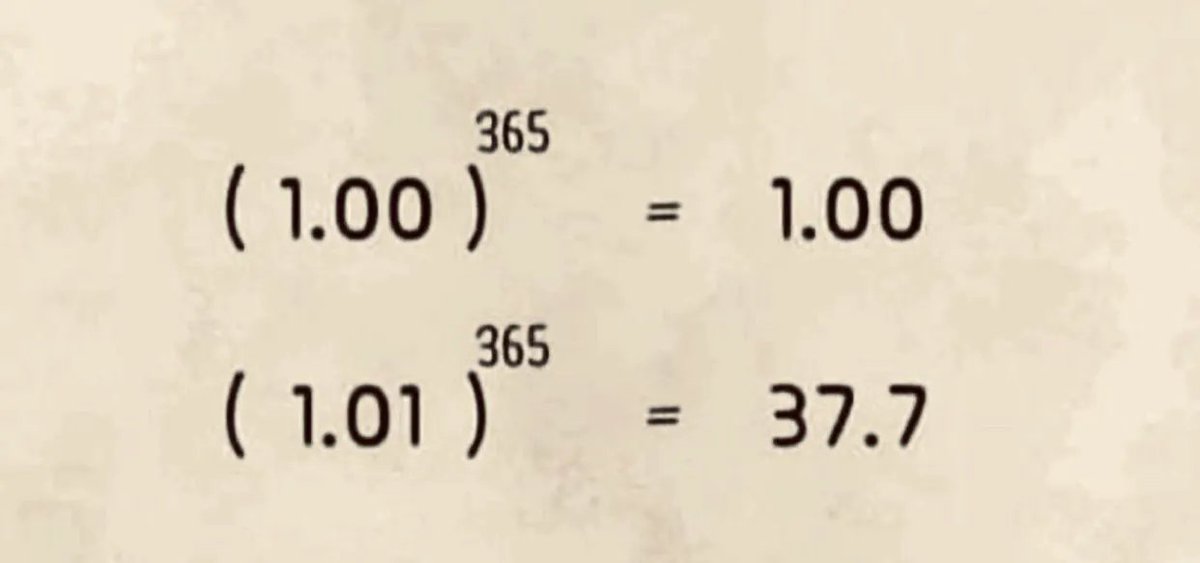Compounding is the eighth wonder of the world.
Those who understand it, earn it. Those who don’t, pay it.
Here's everything you need to know:
Those who understand it, earn it. Those who don’t, pay it.
Here's everything you need to know:
1️⃣ A penny that doubles every day
Let’s say that you have the choice between two sums of money:
▪️$1 million in cash
▪️A penny that doubles every day for a month
Which one would you choose?
Let’s say that you have the choice between two sums of money:
▪️$1 million in cash
▪️A penny that doubles every day for a month
Which one would you choose?
Does the above sound like a difficult question to you?
Let’s give you a hint.
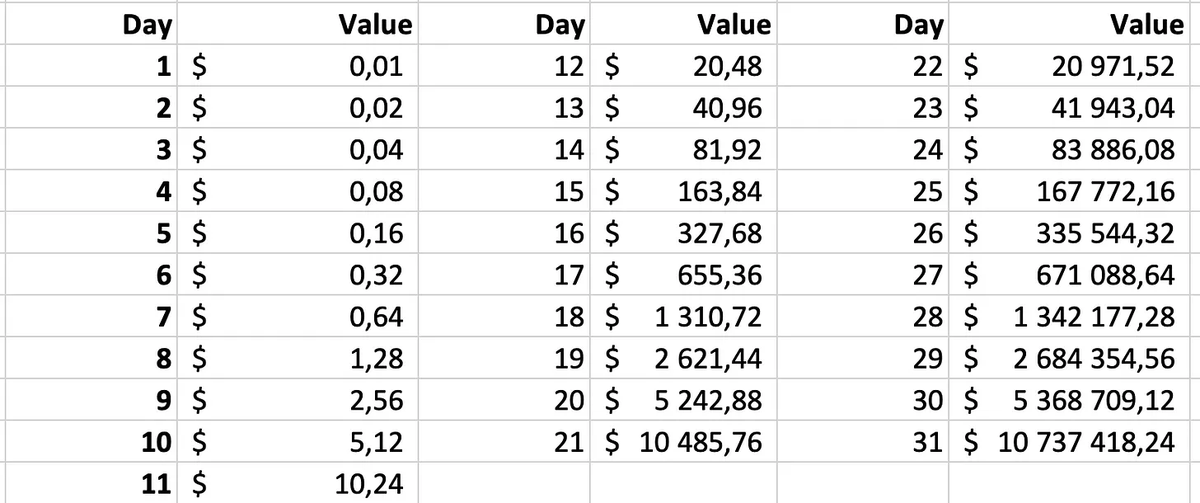
A penny that doubles every day would be worth $0.16 on day 5 and $5.12 on day 10.
Let’s give you a hint.
A penny that doubles every day would be worth $0.16 on day 5 and $5.12 on day 10.
You will probably know that a penny that doubles for a month will be worth more than $1 million. Why else would I ask you this question?
Well, a penny that doubles 30 times would be worth more than $10.7 million!
Here's the math:
Well, a penny that doubles 30 times would be worth more than $10.7 million!
Here's the math:
Please note that in this example it took until the 27th day (!) for the penny to be worth more than $1 million.
The fact that it took until the 27th day shows you why patience and a long-term perspective are crucial to let the compounding work like magic.
The fact that it took until the 27th day shows you why patience and a long-term perspective are crucial to let the compounding work like magic.
Compounding works like magic for investing, but also for other aspects in life.
When you get 1% better every single day for a year, your yearly growth would be equal to 37.7x.
When you get 1% better every single day for a year, your yearly growth would be equal to 37.7x.
2️⃣ Compounding explained
You’ve already learned that compound interest is the eighth wonder of the world.
Compounding works like a snowball. It starts very slow, but the longer you keep rolling, the bigger it gets.
You’ve already learned that compound interest is the eighth wonder of the world.
Compounding works like a snowball. It starts very slow, but the longer you keep rolling, the bigger it gets.
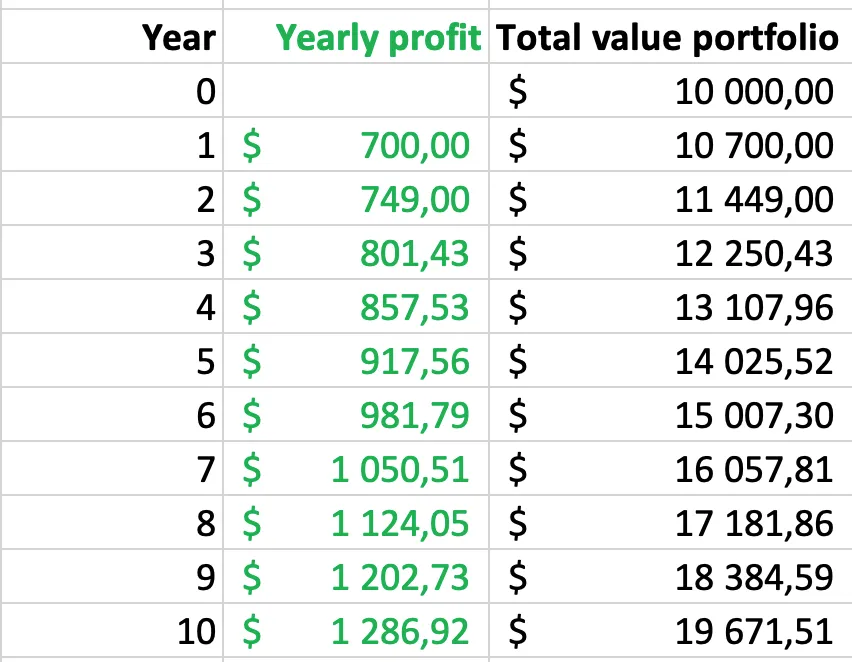
Let’s say that you invest $10,000 and you are able to compound your money at 7% per year.
In year 1, you’ll make $700 ($10,000 * 7%). As a result, the value of your portfolio is equal to $10,700.
In year 1, you’ll make $700 ($10,000 * 7%). As a result, the value of your portfolio is equal to $10,700.
In year 2, you’ll make more than $700. Why? Because you also make money on the $700 you earned the year before. As a result, you’ll make $749 ($10,700 * 7%) in year 2 and the value of your portfolio increases to $11,449.
After 10 years, you’ll even make $1,286.92 (!). This is almost twice as much as in the first year.
When you would invest for very long periods of time (> 20 years), something magical happens.
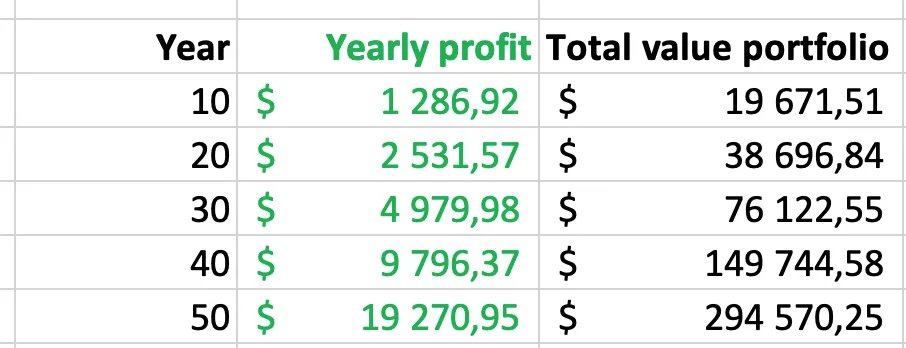
Remember that you made $700 in year 1 and $1,286.92 in year 10.
Remember that you made $700 in year 1 and $1,286.92 in year 10.
Here’s what happens if you keep investing:
▪️ In year 20, you'll gain $2,531.57
▪️ In year 30, you'll gain $4,979.98
▪️ In year 40, you'll gain $9,796.37
▪️ In year 50, you'll gain $19,270.95
▪️ In year 20, you'll gain $2,531.57
▪️ In year 30, you'll gain $4,979.98
▪️ In year 40, you'll gain $9,796.37
▪️ In year 50, you'll gain $19,270.95
If you would keep your $10,000 investment for 50 years, your investment would almost be worth $300,000!
Furthermore, your yearly profit of $19,270.95 would almost be twice as much as what you invested in the first place.
Furthermore, your yearly profit of $19,270.95 would almost be twice as much as what you invested in the first place.
3️⃣ Formula compound interest
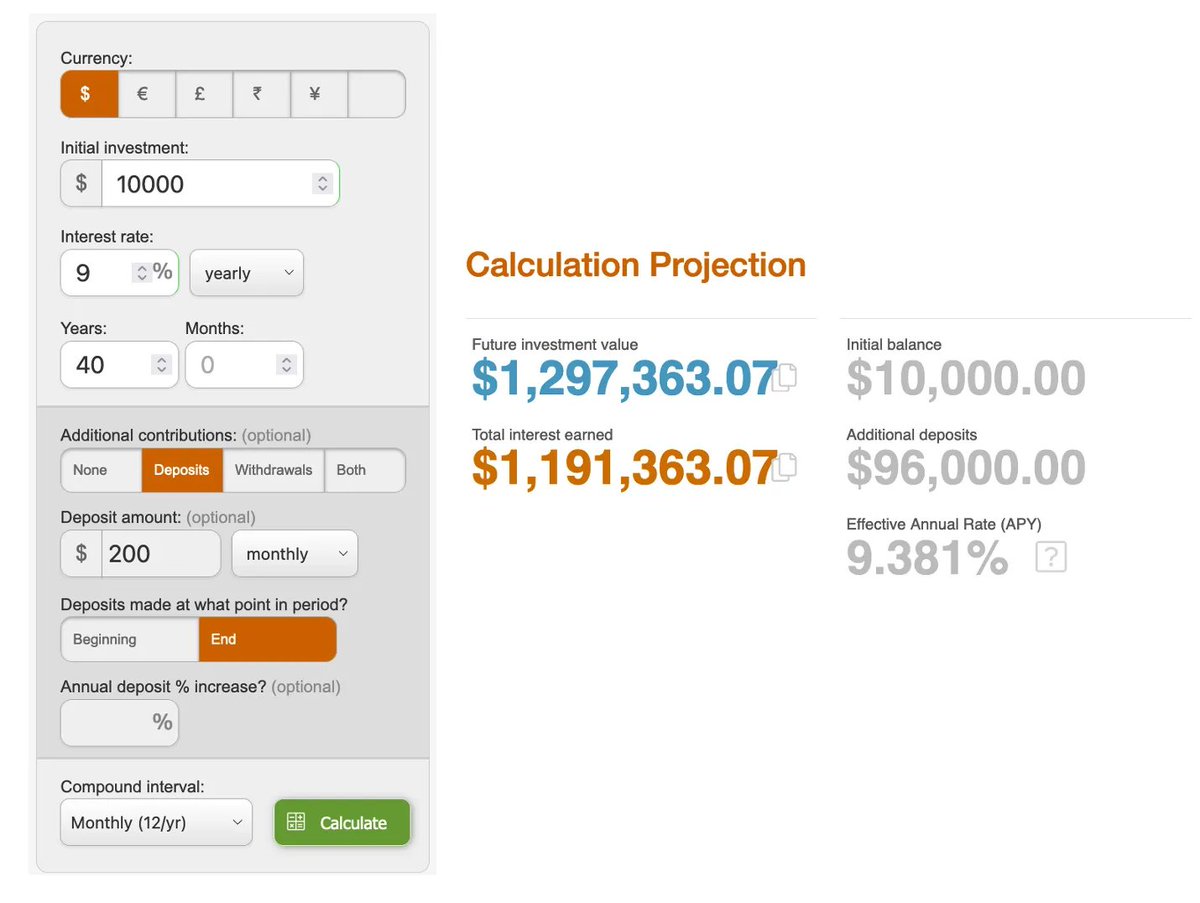
On the internet, there are a lot of compound interest calculators you can use. The Calculator Site is a good example.
On the internet, there are a lot of compound interest calculators you can use. The Calculator Site is a good example.
Here’s an example where you would invest $10,000 at 9% per year for 40 years while adding $200 per month to your investment account (total investment of $106,000 over 40 years).
When you would do this, you would have $1.3 million after 40 years, as you can see here:
When you would do this, you would have $1.3 million after 40 years, as you can see here:
Obviously, you can also calculate it yourself.
Here is the formula for compound interest:
Final amount = beginning amount * (1 + yearly return)^number of periods
Here is the formula for compound interest:
Final amount = beginning amount * (1 + yearly return)^number of periods
If you would invest $10,000 for 20 years at a yearly return of 9%, it would look as follows:
Final amount = $10,000 * (1,09)^20
Final amount = $56,044
Final amount = $10,000 * (1,09)^20
Final amount = $56,044
In the table below, you can find out how many times your wealth compounds at various combinations of yearly returns and years.
When you can for example achieve a yearly return of 12% for 30 years, your money will increase 30-fold (!).
When you can for example achieve a yearly return of 12% for 30 years, your money will increase 30-fold (!).
4️⃣ Start as early as possible
You’ve learned that the longer you can compound your money, the better.
This also means that the sooner you start investing, the longer compounding can work like magic for you.
You’ve learned that the longer you can compound your money, the better.
This also means that the sooner you start investing, the longer compounding can work like magic for you.
Let’s use an example to make this even more clear.
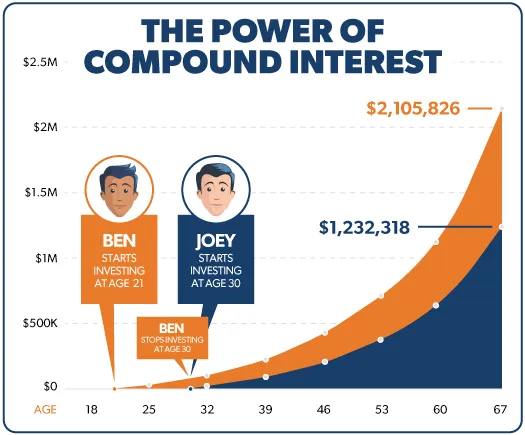
In our example we have 2 men (Ben and Joey) who start investing:
Ben
- Starts investing at age 21
- Monthly investment: $200
- Stops contributing money at age 30 (added money to his account for 9 years)
In our example we have 2 men (Ben and Joey) who start investing:
Ben
- Starts investing at age 21
- Monthly investment: $200
- Stops contributing money at age 30 (added money to his account for 9 years)
Joey
- Starts investing at age 30
- Monthly investment: $200
- Keeps investing until age 67 (added money to his account for 37 years)
In total, Ben will have contributed $21,600 while Joey will have contributed $88,800 to their investment account.
- Starts investing at age 30
- Monthly investment: $200
- Keeps investing until age 67 (added money to his account for 37 years)
In total, Ben will have contributed $21,600 while Joey will have contributed $88,800 to their investment account.
When Ben and Joey both keep their investment until age 67 and manage to compound at an average annual return of 11%, Ben would have $2.1 million while Joey would have grown his account to $1.2 million.
This means that Ben would have almost twice as much money as Joey while he contributed only one-fourth of what Joey contributed!
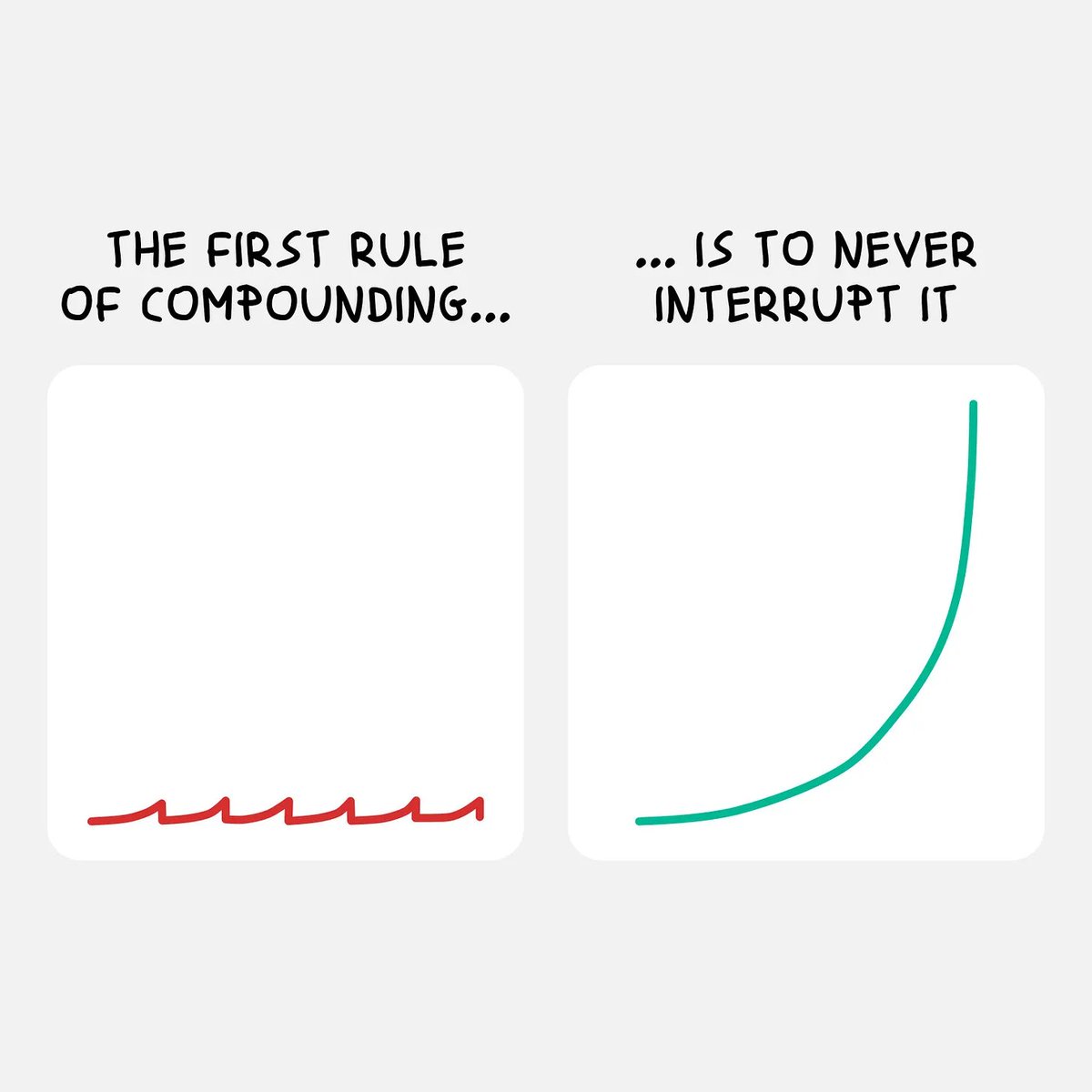
5️⃣ Never interrupt compounding
Charlie Munger once said that the first rule of compounding is to never interrupt it unnecessarily.
You don’t believe Charlie?
You should. Let’s use one more example.
Charlie Munger once said that the first rule of compounding is to never interrupt it unnecessarily.
You don’t believe Charlie?
You should. Let’s use one more example.
Olivier
- Starts investing at age 21
- Monthly investment: $200
Emma
- Starts investing at age 21
- Monthly investments: $200
- Stops investing at age 30 and starts again at age 40
- Starts investing at age 21
- Monthly investment: $200
Emma
- Starts investing at age 21
- Monthly investments: $200
- Stops investing at age 30 and starts again at age 40
This is how their wealth would like if they both keep investing until age 67 and achieve a yearly return of 11%:
- Olivier: $3,3 million
- Emma: $1,1 million
- Olivier: $3,3 million
- Emma: $1,1 million
As you can see, Olivier would have 3 times as much money as Emma just because Emma decided to stop investing for 10 years.
6️⃣ Conclusion
That’s it for today. Here’s what you should remember:
- Compound interest is the eight wonder of the world
- Start investing as early as possible
- You can calculate compound interest via this formula:
That’s it for today. Here’s what you should remember:
- Compound interest is the eight wonder of the world
- Start investing as early as possible
- You can calculate compound interest via this formula:
If you liked this, you'll love our free course.
The course will teach you how to read Financial Statements like a professional.
Sign up here to receive it:
eepurl.com
The course will teach you how to read Financial Statements like a professional.
Sign up here to receive it:
eepurl.com
Loading suggestions...