لمضاعفة رأس مالك 100% بعائد سنوي 10% ستستغرق 7.2 سنوات و أحيانا أقل.
هنا تأتي فائدة العائد المركب في تسارع نمو الأرباح مع الوقت.
هناك قاعدة تسمى "قاعدة 72" تستخدم لتوقع المدة الزمنية لمضاعفة رأس المال.
في هذه السلسلة سوف نقوم بشرح "قاعدة 72" وكيفية استخدامها لفهم العائد المركب
هنا تأتي فائدة العائد المركب في تسارع نمو الأرباح مع الوقت.
هناك قاعدة تسمى "قاعدة 72" تستخدم لتوقع المدة الزمنية لمضاعفة رأس المال.
في هذه السلسلة سوف نقوم بشرح "قاعدة 72" وكيفية استخدامها لفهم العائد المركب
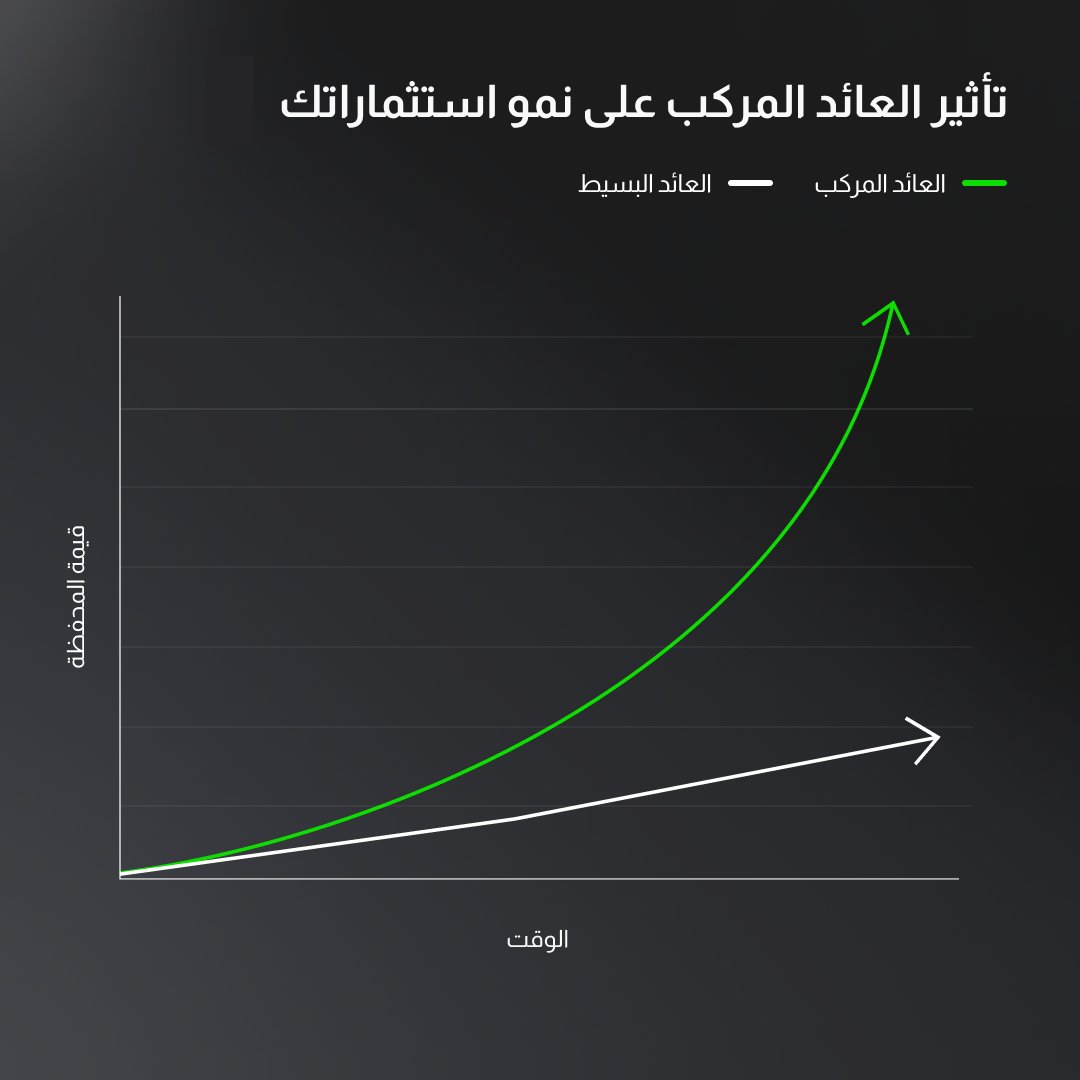
بداية، يجب أن تعرف أن هناك نوعين من العوائد في الاستثمار:
- العائد البسيط (خطي) Linear: وهو أن تحقق ربح بنسبة ثابتة على رأس المال.
مثال، نسبة الربح السنوية Coupon التي تربحها من الصكوك/السندات.
فمثلًا، لو استثمرت 1,000 ريال في صك بعائد 3% لمدة 10 سنوات، ستربح 30 ريال سنويًا!
- العائد البسيط (خطي) Linear: وهو أن تحقق ربح بنسبة ثابتة على رأس المال.
مثال، نسبة الربح السنوية Coupon التي تربحها من الصكوك/السندات.
فمثلًا، لو استثمرت 1,000 ريال في صك بعائد 3% لمدة 10 سنوات، ستربح 30 ريال سنويًا!
- العائد المركب (أسّي) Exponential: وهو الربح على رأس المال الأساسي + الأرباح.
مثال: عندما تقوم بالاستثمار في الأسهم والحصول على توزيعات أرباح نقدية وإعادة استثمارها.
بذلك تستفيد من العائد المركب في تعظيم أرباحك عن طريق الحصول على ربح على رأس المال و الأرباح.
مثال: عندما تقوم بالاستثمار في الأسهم والحصول على توزيعات أرباح نقدية وإعادة استثمارها.
بذلك تستفيد من العائد المركب في تعظيم أرباحك عن طريق الحصول على ربح على رأس المال و الأرباح.
كمستثمرين نميل إلى التفكير بشكل "خطي" Linear في أغلب الأحيان لأن ذلك يساعدنا على استيعاب التغيير بشكل أسرع.
لكن!
في الاستثمار يجب أن تفكر بشكل مركب "أسّي" وليس "خطي".
وذلك لأن العوائد الاستثمارية تنمو بشكل مركب مع مرور الوقت.
النمو لا يحصل بوتيرة ثابتة بل يتسارع مع الوقت.
لكن!
في الاستثمار يجب أن تفكر بشكل مركب "أسّي" وليس "خطي".
وذلك لأن العوائد الاستثمارية تنمو بشكل مركب مع مرور الوقت.
النمو لا يحصل بوتيرة ثابتة بل يتسارع مع الوقت.
واحدة من المعادلات التي ستساعدك على فهم "العائد المركب" بشكل سريع ومباشر هي:
"قاعدة 72"
تساعدك هذه القاعدة على فهم العائد المركب بشكل بسيط و سهل.
تسهل عليك طريقة حساب العائد المركب بمعادلة لحساب عدد السنوات المطلوبة لمضاعفة رأس مالك (100%) بناء على عائد الاستثمار المعطى.
"قاعدة 72"
تساعدك هذه القاعدة على فهم العائد المركب بشكل بسيط و سهل.
تسهل عليك طريقة حساب العائد المركب بمعادلة لحساب عدد السنوات المطلوبة لمضاعفة رأس مالك (100%) بناء على عائد الاستثمار المعطى.
إذًا ما هي "قاعدة 72"؟
هي معادلة حسابية يمكن استخدامها لحساب عدد السنوات التي سوف تستغرقها لمضاعفة رأس مالك المستثمر 100% بناء على العائد المتوقع على الاستثمار.
و صيغتها كالتالي:
72 \ العائد السنوي على الاستثمار ≈ عدد السنوات لمضاعفة رأس المال.
هي معادلة حسابية يمكن استخدامها لحساب عدد السنوات التي سوف تستغرقها لمضاعفة رأس مالك المستثمر 100% بناء على العائد المتوقع على الاستثمار.
و صيغتها كالتالي:
72 \ العائد السنوي على الاستثمار ≈ عدد السنوات لمضاعفة رأس المال.
كما هو موضح في الصورة في التغريدة السابقة، العائد السنوي على الاستثمار موجود في المقام.
لذلك يمكنك استنتاج التالي:
- كلما ارتفع المقام (العائد السنوي) انخفض الناتج وبالتالي عدد السنوات.
- كلما انخفض المقام (العائد السنوي) ارتفع الناتج وبالتالي عدد السنوات.
لذلك يمكنك استنتاج التالي:
- كلما ارتفع المقام (العائد السنوي) انخفض الناتج وبالتالي عدد السنوات.
- كلما انخفض المقام (العائد السنوي) ارتفع الناتج وبالتالي عدد السنوات.
كذلك من المهم معرفة أن رأس المال هنا ليس له علاقة بالقاعدة الحسابية.
بمعنى، إذا تمكنت من تحقيق عائد سنوي 10% ستتمكن من مضاعفة رأس مالك خلال 72\10 ≈ 7.2 سنوات.
سواء كان رأس مالك 1000 ريال أو 100 مليون ريال، ستتمكن من مضاعفة المبلغ خلال نفس الفترة بناء على العائد السنوي.
بمعنى، إذا تمكنت من تحقيق عائد سنوي 10% ستتمكن من مضاعفة رأس مالك خلال 72\10 ≈ 7.2 سنوات.
سواء كان رأس مالك 1000 ريال أو 100 مليون ريال، ستتمكن من مضاعفة المبلغ خلال نفس الفترة بناء على العائد السنوي.
لنفترض على سبيل المثال انك قمت باستثمار مبلغ 10,000 ريال بمتوسط عائد سنوي 15% لمدة 50 سنة.
السؤال هو، ما هي المحصلة النهائية لقيمة 10,000 ريال بعد 50 سنة؟
يمكن حل هذا السؤال لإيجاد إجابة تقريبية باستخدام "قاعدة 72" واستخدام أسلوب المضاعفات في الحساب في 3 خطوات:
السؤال هو، ما هي المحصلة النهائية لقيمة 10,000 ريال بعد 50 سنة؟
يمكن حل هذا السؤال لإيجاد إجابة تقريبية باستخدام "قاعدة 72" واستخدام أسلوب المضاعفات في الحساب في 3 خطوات:
1\
إذا كان العائد السنوي المتوقع هو 15%، إذًا باستخدام "قاعدة 72" يمكن حساب عدد السنوات التي ستحتاجها لمضاعفة رأس مالك:
72 \ 15 ≈ 5 سنوات
إذا كان العائد السنوي المتوقع هو 15%، إذًا باستخدام "قاعدة 72" يمكن حساب عدد السنوات التي ستحتاجها لمضاعفة رأس مالك:
72 \ 15 ≈ 5 سنوات
2\
خلال 50 سنة ستتمكن من مضاعفة أموالك تقريبا 10 مرات Folds (من إجمالي القيمة):
50 (سنة) \ 5 (عدد السنوات لكل مضاعف) ≈ 10 مضاعفات
خلال 50 سنة ستتمكن من مضاعفة أموالك تقريبا 10 مرات Folds (من إجمالي القيمة):
50 (سنة) \ 5 (عدد السنوات لكل مضاعف) ≈ 10 مضاعفات
3\
إذا تمكنت من مضاعفة قيمة محفظتك 10 مرات فإنك ستتمكن من مضاعفة قيمة كل 1 ريال إلى 1024 ريال.
أي 102400%
أو 1024X ضعف.
إذا تمكنت من مضاعفة قيمة محفظتك 10 مرات فإنك ستتمكن من مضاعفة قيمة كل 1 ريال إلى 1024 ريال.
أي 102400%
أو 1024X ضعف.
لو بدأت بمبلغ 10,000 ريال و تمكنت من تحقيق عائد سنوي 15% ستكون قيمة استثمارك بعد 50 سنة 10.2 مليون.
كيف؟ انظر الجدول التالي.
كيف؟ انظر الجدول التالي.
هل معادلة "قاعدة 72" تعطي نتائج دقيقة عند الحساب؟
"قاعدة 72" تعطي نتائج دقيقة جدًا خصوصًا للعوائد الواقعة في نطاق 6%-10%.
و لكن لدقة إضافية في الحساب عند التعامل مع عوائد خارج هذا النطاق، يمكن تعديل المعادلة ليتم إضافة/طرح 1 من رقم 72 لكل 3 نسب مئوية في أي اتجاه من عائد 8%.
"قاعدة 72" تعطي نتائج دقيقة جدًا خصوصًا للعوائد الواقعة في نطاق 6%-10%.
و لكن لدقة إضافية في الحساب عند التعامل مع عوائد خارج هذا النطاق، يمكن تعديل المعادلة ليتم إضافة/طرح 1 من رقم 72 لكل 3 نسب مئوية في أي اتجاه من عائد 8%.
لذلك، اذا أردت حساب عدد السنوات لمضاعفة استثمارك بعائد سنوي 11% (3% زيادة عن 8%) يجب إضافة 1 ليصبح الرقم 73 لدقة حسابية أعلى.
إذا أردت حساب المدة الزمنية لعائد 14% فيجب إضافة 2 (6 نسب مئوية أعلى من 8%) ليصبح الرقم 74 لدقة حسابية أعلى.
ويتم طرح 1 إذا كان العائد 5% و هكذا.
إذا أردت حساب المدة الزمنية لعائد 14% فيجب إضافة 2 (6 نسب مئوية أعلى من 8%) ليصبح الرقم 74 لدقة حسابية أعلى.
ويتم طرح 1 إذا كان العائد 5% و هكذا.
المستثمر المعروف وارين بافيت هو أحد أثرى أثرياء العالم وتمكن من تكوين ثروته عن طريق الاستفادة من العائد المركب.
تمكن وارين بافيت من تحقيق متوسط عائد سنوي 20% على مدى 57 عام عندما استحوذ على بيركشاير هاثاوي في 1965.
يعني ذلك أن بافيت تمكن من مضاعفة أمواله مرة كل 4 سنوات تقريبا!
تمكن وارين بافيت من تحقيق متوسط عائد سنوي 20% على مدى 57 عام عندما استحوذ على بيركشاير هاثاوي في 1965.
يعني ذلك أن بافيت تمكن من مضاعفة أمواله مرة كل 4 سنوات تقريبا!
على مدى 57 عام تمكن من مضاعفة أمواله 55 \ 4 ≈ 14 مرة تقريبًا.
معدل نمو المحفظة بعد 14 ضعف سيكون 2^14 ≈ 16,384X
أو %1,638,400
نمو بهذا المعدل سيحول 10,000 ريال إلى 163,840,000 ريال.
معدل نمو المحفظة بعد 14 ضعف سيكون 2^14 ≈ 16,384X
أو %1,638,400
نمو بهذا المعدل سيحول 10,000 ريال إلى 163,840,000 ريال.
أخيرًا، "قاعدة 72" ستساعدك في استيعاب العائد المركب عن طريق الحساب بالمضاعفات والمكررات.
وذلك لأن الفائدة العظمى في الاستثمار تكمن في تعظيم الأرباح عن طريق العائد المركب حيث يؤدي لتسارع نمو الأرباح مع الوقت.
أو كما أطلق عليها Albert Einstein: "العجيبة الثامنة من عجائب الدنيا".
وذلك لأن الفائدة العظمى في الاستثمار تكمن في تعظيم الأرباح عن طريق العائد المركب حيث يؤدي لتسارع نمو الأرباح مع الوقت.
أو كما أطلق عليها Albert Einstein: "العجيبة الثامنة من عجائب الدنيا".
شكراً للقراءة!
إذا أعجبتك السلسلة قم بمتابعة حسابنا @Getbaraka للمزيد من المحتوى المالي والأخبار المالية!
إذا أعجبتك السلسلة قم بمتابعة حسابنا @Getbaraka للمزيد من المحتوى المالي والأخبار المالية!
جاري تحميل الاقتراحات...