كثيرًا ما نستخدم في حواراتنا مقولة: ”Correlation doesn’t imply causation“ أو ”الارتباط لا يعني السببية“ عندما نريد أن نقول أن حدوث شيئين في نفس الوقت لا يعني أن أحدهما أدى إلى حصول الآخر
قد لا نستطيع أن نعرف المسببات في البيانات لدينا، ولكن نستطيع أن نقيس مدى الارتباط بينها 🤛🤜
قد لا نستطيع أن نعرف المسببات في البيانات لدينا، ولكن نستطيع أن نقيس مدى الارتباط بينها 🤛🤜
على سبيل المثال، إذا كان لدينا بيانات لمستوى الطلاب الدراسي وكنا مهتمين بالتنبؤ بدرجاتهم النهائية بناء على خصائص مثل العمر ووجود اتصال بالإنترنت في المنزل وغيرها 📶
فإننا يمكن أولًا دراسة العلاقات بين هذه الخصائص والدرجة النهائية لنعرف أي منها أكثر تأثيرًا في تحديد الدرجة 💯
فإننا يمكن أولًا دراسة العلاقات بين هذه الخصائص والدرجة النهائية لنعرف أي منها أكثر تأثيرًا في تحديد الدرجة 💯
ولكن قبل ذلك، ماذا يعني عندما نقول أن هناك ترابط أو correlation بين متغيرَين؟ 🤔
إذا رسمنا مخطط انتشار أو Scatter plot للمتغيريَن ولاحظنا وجود نمط في توزيع النقاط أو شكل مميز فهذا يدل على وجود ترابط، إما أن يكون خطي (كلما زاد متغير أو نقص، تغير الآخر بمعدل ثابت) أو غير خطي.
إذا رسمنا مخطط انتشار أو Scatter plot للمتغيريَن ولاحظنا وجود نمط في توزيع النقاط أو شكل مميز فهذا يدل على وجود ترابط، إما أن يكون خطي (كلما زاد متغير أو نقص، تغير الآخر بمعدل ثابت) أو غير خطي.
في الإحصاء، يوجد العديد من الطرق والأساليب لقياس مدى الترابط والاعتماد بين المتغيرات العشوائية. أشهرها هو معامل الترابط الخطي Pearson، ويتراوح قِيَمه بين سالب واحد وموجب واحد.
تذكر📝: معامل Pearson هو لقياس العلاقة الخطية، وقد لا يتمكن من الكشف عن العلاقات الغير خطية.
تذكر📝: معامل Pearson هو لقياس العلاقة الخطية، وقد لا يتمكن من الكشف عن العلاقات الغير خطية.
تُوفر مكتبة Pandas في بايثون دالة لحساب الترابط بين المتغيرات في البيانات باستخدام مقاييس إحصائية متنوعة:
١- مُعامل Pearson: لقياس ترابط الخطي فقط.
٢- مُعامل Spearman: للترابط الخطي والغير خطي أيضًا.
٣- مُعامل Kendall: مشابه ل Spearman، ويعطي غالبًا نتائج أفضل منه.
١- مُعامل Pearson: لقياس ترابط الخطي فقط.
٢- مُعامل Spearman: للترابط الخطي والغير خطي أيضًا.
٣- مُعامل Kendall: مشابه ل Spearman، ويعطي غالبًا نتائج أفضل منه.
إذا استخدمنا هذه الدالة من Pandas على بيانات درجات الطلاب، فإن الناتج هو مصفوفة تحوي على قيم الترابط بين كل متغير وآخر.
لاحظ أن هناك ترابط سالب ضعيف بين العمر ودرجة الطالب (0.16-)، وهذا يعني ربما أنه كلما صعد الطالب إلى مراحل دراسية أعلى، زادت صعوبة الاختبارات وقلّت الدرجة.
لاحظ أن هناك ترابط سالب ضعيف بين العمر ودرجة الطالب (0.16-)، وهذا يعني ربما أنه كلما صعد الطالب إلى مراحل دراسية أعلى، زادت صعوبة الاختبارات وقلّت الدرجة.
لكن إذا تمعّنا في مصفوفة الترابط أكثر، سنجد أنها تفقد بعض الخصائص في البيانات الأساسية كولي الأمر ووجود إنترنت في المنزل.
لماذا لم تقم دالة حساب الترابط في Pandas بأخذها بعين الاعتبار؟ 🤔
لماذا لم تقم دالة حساب الترابط في Pandas بأخذها بعين الاعتبار؟ 🤔
معلومة على الماشي 🚶
هناك نوعان أساسيان من البيانات: بيانات عددية، وأخرى نوعية أو وصفية. العددية تأخذ قيمًا أو أرقامًا مثل الطول، عدد الإخوة، وساعات المذاكرة. أما النوعية فتتكون من أصناف محددة أو أنواع قد لا تكون مرتبة أو بينها أي علاقة مثل المدينة أو موديل السيارة.
هناك نوعان أساسيان من البيانات: بيانات عددية، وأخرى نوعية أو وصفية. العددية تأخذ قيمًا أو أرقامًا مثل الطول، عدد الإخوة، وساعات المذاكرة. أما النوعية فتتكون من أصناف محددة أو أنواع قد لا تكون مرتبة أو بينها أي علاقة مثل المدينة أو موديل السيارة.
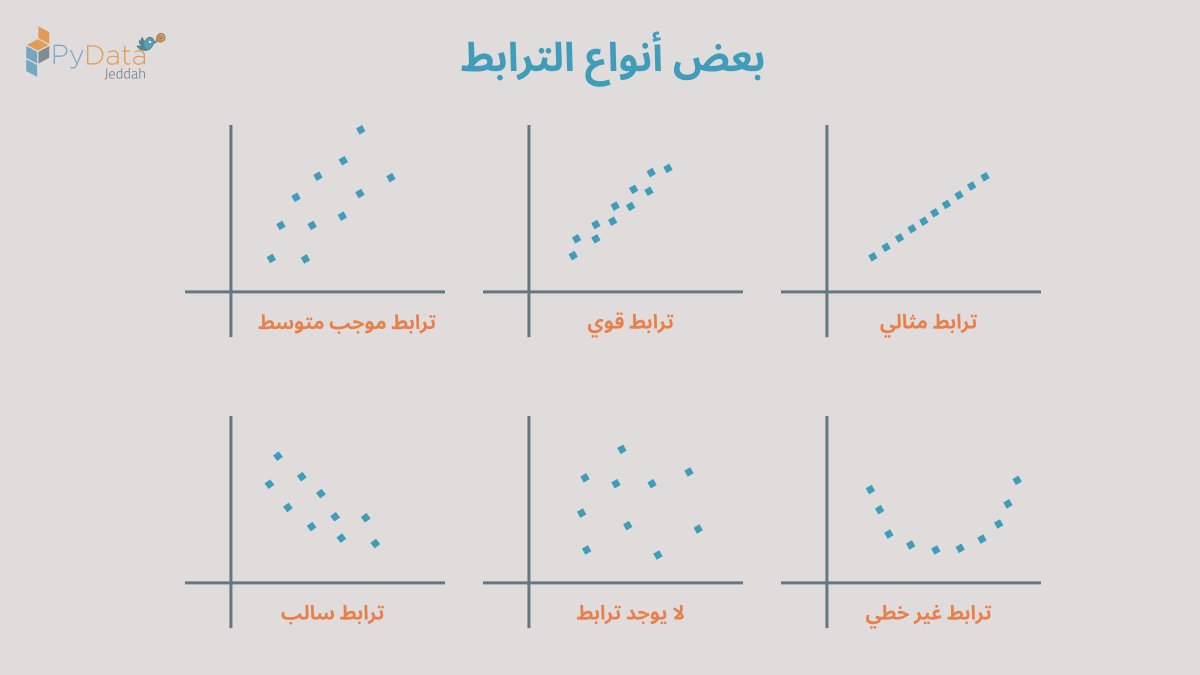
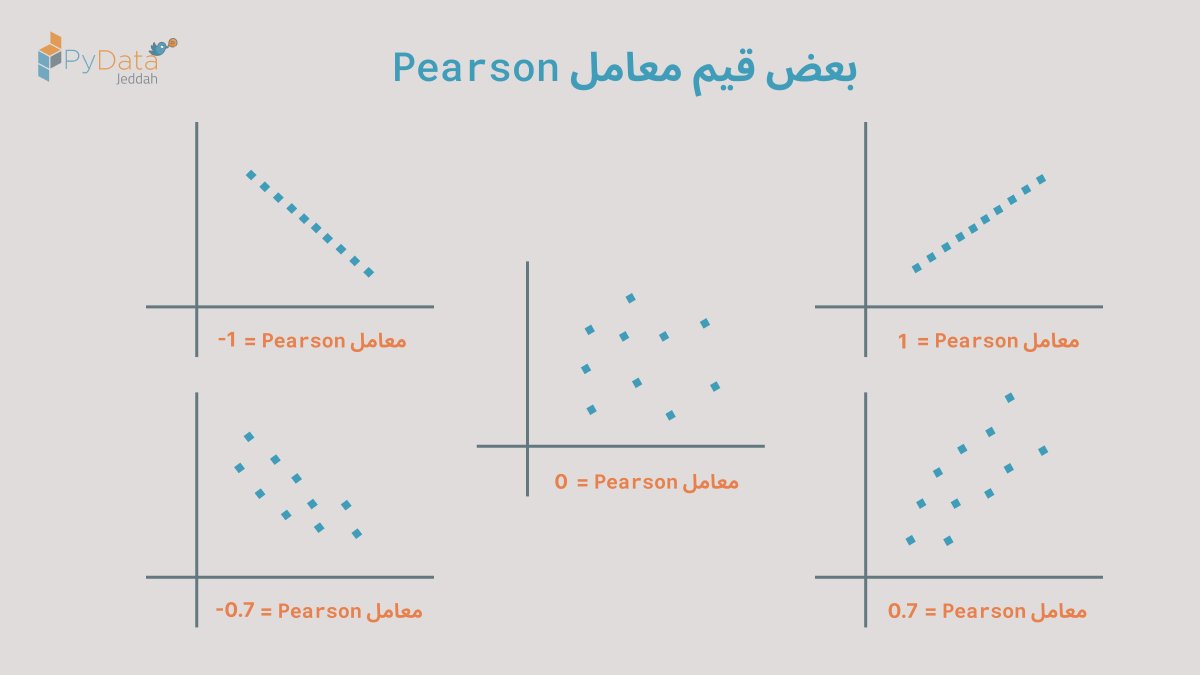
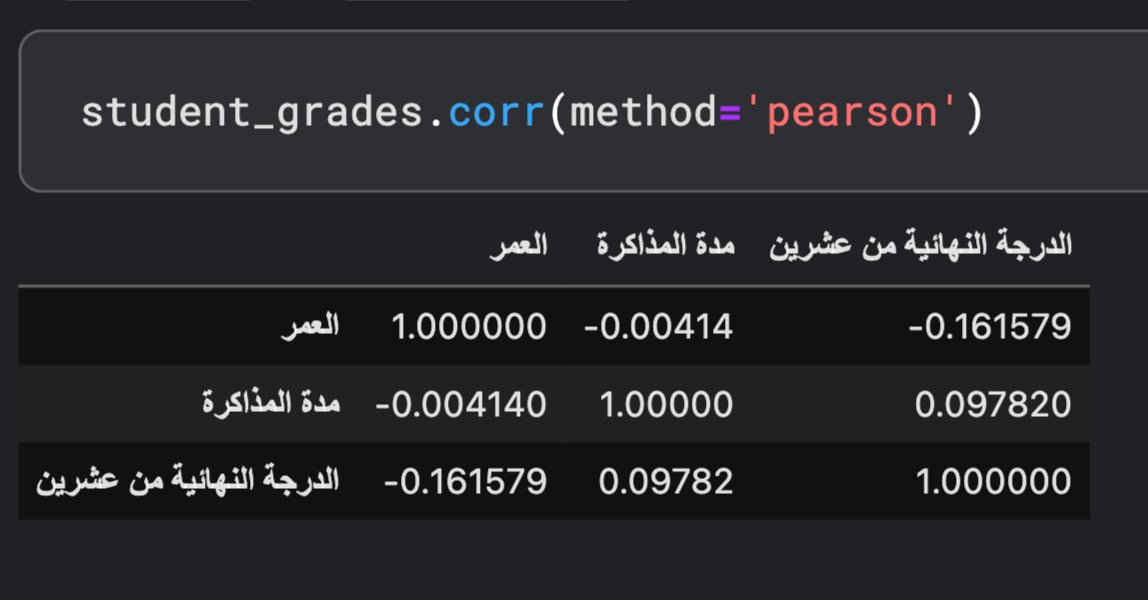
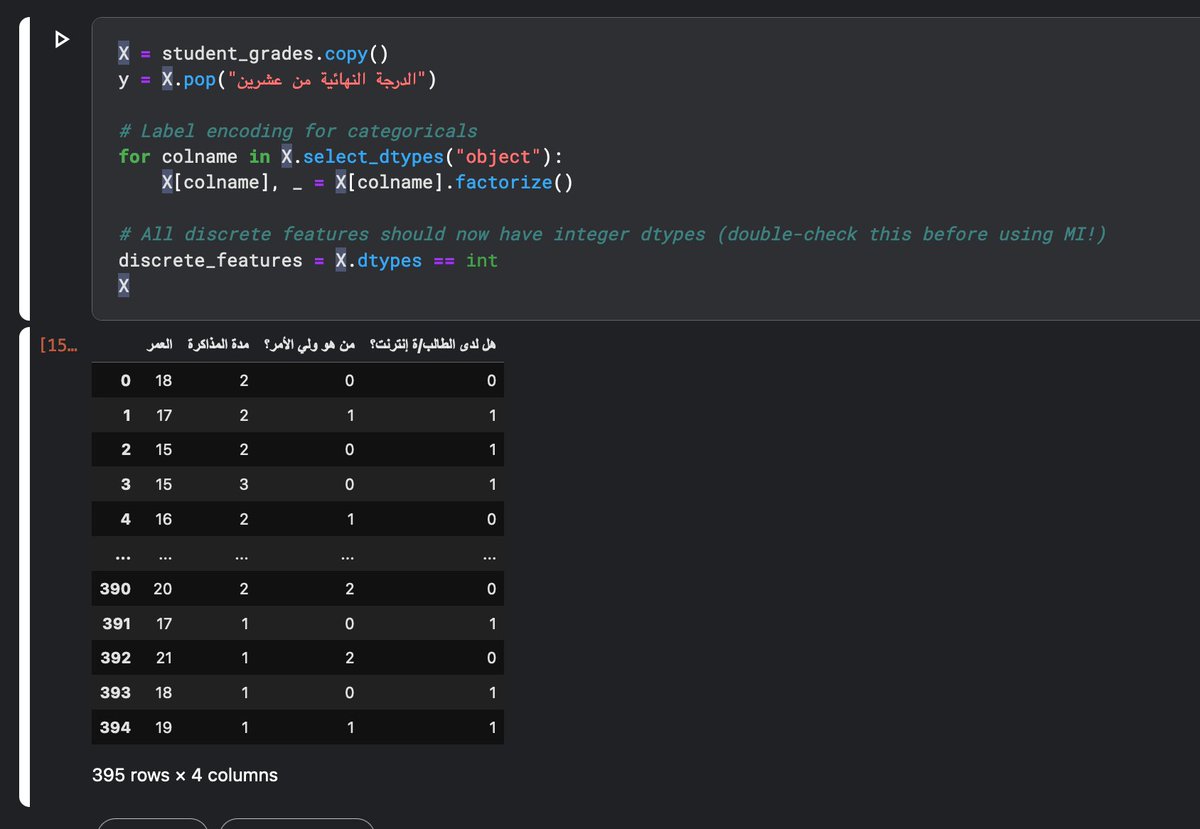
الإجابة هي أنه لا يمكن حساب الترابط بين متغيريَن باستخدام الطرق المذكورة إذا كان أحدهما وصفيًا، لأن المتغيرات الوصفية لا تتبع أحيانًا ترتيبًا محددًا كولي الأمر ووجود الإنترنت.
لكن في حالات أخرى يكون هناك ترتيب كتقييمات المطاعم، ويمكن حينها تمثيلها كبيانات عددية، وحساب الترابط.
لكن في حالات أخرى يكون هناك ترتيب كتقييمات المطاعم، ويمكن حينها تمثيلها كبيانات عددية، وحساب الترابط.
فما الحل إذن؟ 🧐
يوجد مقياس آخر يدعى Mutual Information ، وهو يقيس إلى أي مدى ستكون واثق من القيمة المحتملة لمتغير بمجرد معرفتك قيمة المتغير الآخر.
المزايا في هذا المقياس أنه يحسب قوة العلاقة أو الاعتمادية بين متغيرَين بغض النظر عن نوعيهما، ويستطيع الكشف عن أي نوع علاقة.
يوجد مقياس آخر يدعى Mutual Information ، وهو يقيس إلى أي مدى ستكون واثق من القيمة المحتملة لمتغير بمجرد معرفتك قيمة المتغير الآخر.
المزايا في هذا المقياس أنه يحسب قوة العلاقة أو الاعتمادية بين متغيرَين بغض النظر عن نوعيهما، ويستطيع الكشف عن أي نوع علاقة.
تقدم مكتبة scikit-learn دالتين لحساب Mutual Information هما mutual_info_classif و mutual_info_regression بناء على نوع المتغير المستهدف في البيانات إذا كان وصفيًا أو كميًا.
بما أننا مهتمون في دراسة العلاقة بين درجة الطالب والمتغيرات الأخرى، لذا سنستخدم mutual_info_regression ✨
بما أننا مهتمون في دراسة العلاقة بين درجة الطالب والمتغيرات الأخرى، لذا سنستخدم mutual_info_regression ✨
لكن قبل ذلك، خلونا نجهز البيانات بتطبيق ال Label Encoding على البيانات الوصفية لدينا. يقوم ال Label Encoder بتحويل الأنواع في البيانات الوصفية إلى أرقام.
على سبيل المثال، عند تطبيقه على المتغير ولي الأمر سيستبدل الأم بصفر، الأب بواحد، وشخص آخر باثنين.
على سبيل المثال، عند تطبيقه على المتغير ولي الأمر سيستبدل الأم بصفر، الأب بواحد، وشخص آخر باثنين.
إذا شغلنا الآن دالة ال Mutual Information على بيانات درجات الطلاب، سوف نجد أنها حَسبت العلاقة بين جميع بيانات الطلاب وبين درجاتهم النهائية، كما أننا سنلاحظ أن العمر هو صاحب أقوى علاقة مع الدرجة النهائية.
تذكر 📝: أن قيم هذا المقياس تتراوح بين صفر (ليس هناك علاقة) وما لانهاية.
تذكر 📝: أن قيم هذا المقياس تتراوح بين صفر (ليس هناك علاقة) وما لانهاية.
في هذه السلسلة، تكلمنا عن الترابط وأنواعه وبعض المقاييس الإحصائية التي تحسبه. لكننا لم نتطرق إلى الشق الآخر من الموضوع:
هل من الممكن أن نقيس ونكشف عن العلاقات السَببية causal relationships ؟ ↩️
خليكم قريبين عشان ما تفوتكم سلاسلنا القادمة، وأعطونا رأيكم عن هذا الثريد 🤗
هل من الممكن أن نقيس ونكشف عن العلاقات السَببية causal relationships ؟ ↩️
خليكم قريبين عشان ما تفوتكم سلاسلنا القادمة، وأعطونا رأيكم عن هذا الثريد 🤗
رابط الكود 🔗: kaggle.com
جاري تحميل الاقتراحات...