ما هي الخوارزميّة ذاتيّة الاستدعاء (recursive algorithm)؟
ببساطة، هي خوارزمية تهدف إلى حلّ المشكلة من خلال استدعاء ذاتها لعدد معيّن من المرّات، بحيث يتعامل كلّ استدعاء مع جزء أصغر من تلك المشكلة (subproblem)، حتى تُحَلّ بالكامل.. تأمّل المثال في الصورة أدناه (بلغة ++C).
(سلسلة)
ببساطة، هي خوارزمية تهدف إلى حلّ المشكلة من خلال استدعاء ذاتها لعدد معيّن من المرّات، بحيث يتعامل كلّ استدعاء مع جزء أصغر من تلك المشكلة (subproblem)، حتى تُحَلّ بالكامل.. تأمّل المثال في الصورة أدناه (بلغة ++C).
(سلسلة)
استخدمنا في هذا المثال دالّة ذاتيّة الاستدعاء (recursive function) وأسميناها "factorial" (من السطر 19 إلى 25)، واسم الدالّة يشير إلى مهمّتها المتمثّلة في حساب مضروب العدد (factorial)، فلو أردنا حساب مضروب العدد ثلاثة (يُكتَب رياضيًّا هكذا: 3!)، فسيكون كالتالي:
3! = 3*2*1 = 6
3! = 3*2*1 = 6
عندما أردنا حساب مضروب العدد برمجيًّا، استخدمنا دالّة ذاتيّة الاستدعاء كما رأينا في الصورة السابقة، بحيث تستقبل هذه الدالّة عددًا صحيحًا، ثم تُوجِد مضروبه من خلال التعليمات المكتوبة في جسمها (function body).. لاحظ أنّ عمليّة استدعاء الدالة لنفسها تحدث في السطر رقم 21..
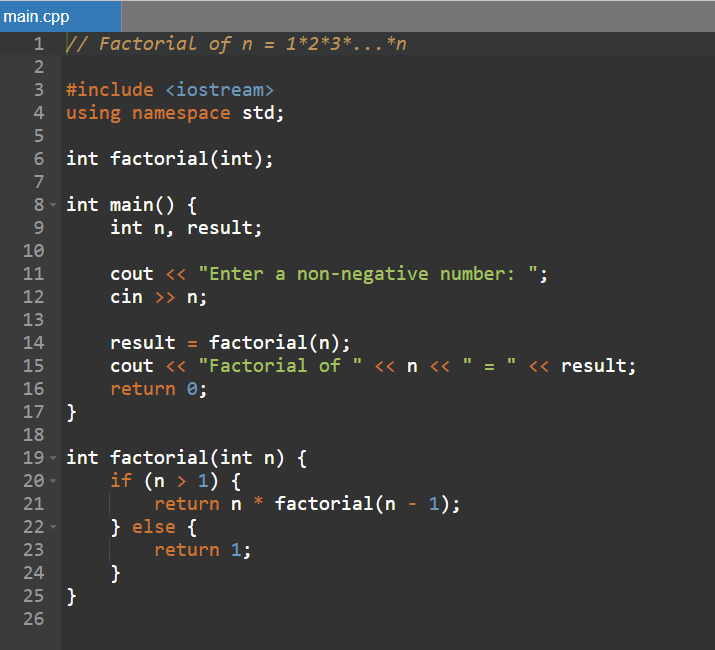
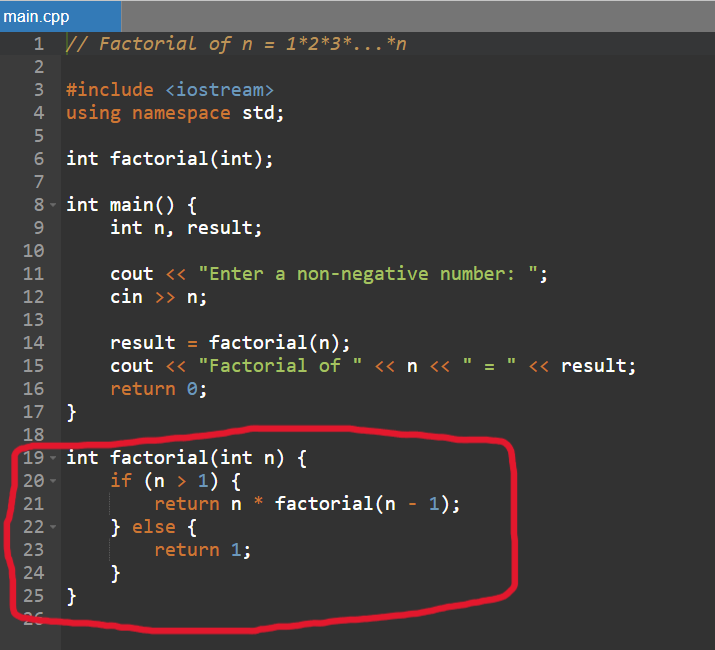
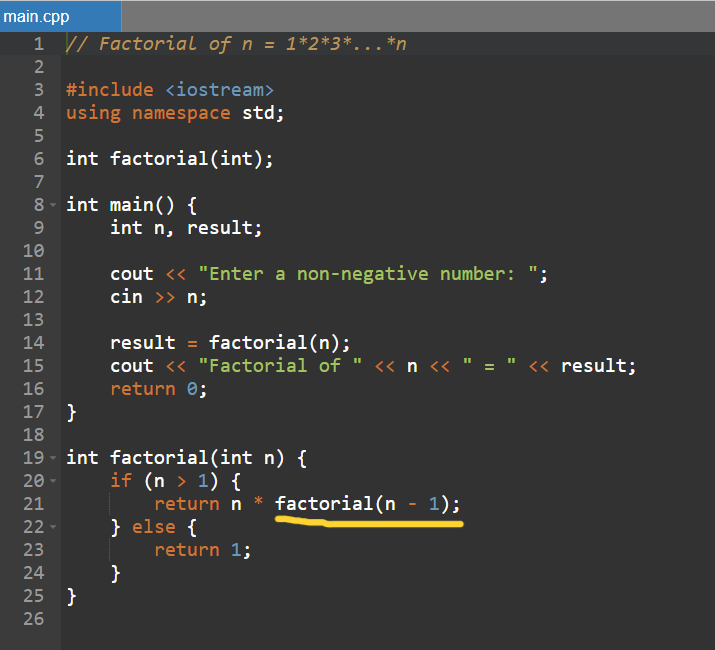
لكنّ معامل (parameter) الدالّة المستدعاة لن يكون العدد نفسه (n)، وإنّما العدد ناقصًا واحد (n - 1)، بحيث يصبح العدد أصغر (مشكلة أصغر)، وهو ما يتوافق مع تعريف الخوارزميّة ذات الاستدعاء الذاتي المذكور في التغريدة الأولى أعلاه، وحتى نفهم طريقة عمل هذا النوع من الدوال، لنأخذ مثالًا..
لنفترض أنّ العدد الداخل إلى الدالّة هو 3 .. في البداية سيتم التحقق ما إذا كان العدد أكبر من 1 (السطر 20)، فإذا كان أكبر من 1 ستُرجِع الدالة العدد بعد ضربه في ناتج استدعاء الدالّة لنفسها لإيجاد ناتج مضروب العدد ناقصًا 1 (السطر 21)، وإلا سترجع 1 (السطر 23). لنتابع..
العدد 3 هو أكبر من 1، إذن فالشرط صحيح (true)، وبالتالي ينبغي أن تُرجِع الدالة ناتج ضرب العدد 3 في ناتج استدعاء الدالة لنفسها لحساب مضروب العدد 3 ناقصًا 1 :
factorial (n - 1) = factorial (3 - 1) = factorial (2)
factorial (n - 1) = factorial (3 - 1) = factorial (2)
الآن ستتوقّف دالّة "factorial (3)" عن العمل مؤقّتًا حتى تنتهي الدالّة "factorial (2)" من عملها وتعود بالناتج الذي سيتم ضربه في العدد 3، وهنا سننتقل إلى دالّة "factorial (2)" لتتبّع الحلّ..
الآن نحن نتعامل مع دالّة أخرى مدخلها هو العدد 2، وسوف يمرّ العدد بالخطوات نفسها التي مرّ بها العدد 3، فهل العدد 2 أكبر من 1 ؟ وبما أنّ الشرط صحيح، فسوف تُرجِع الدالّة ناتج ضرب العدد 2 في ناتج استدعاء الدالّة لنفسها مجدّدًا لحساب مضروب العدد 2 ناقصًا 1:
factorial (n - 1) = factorial (2 - 1) = factorial (1)
وبنفس الطريقة، ستتوقّف الدالّة "factorial (2)" عن العمل مؤقّتًا بانتظار ناتج الدالّة "factorial (1)" حتى يُضرَب في العدد 2.. وسننتقل الآن إلى استدعاء الدالّة الثاني لنفسها، وهي الدالّة "factorial (1)" لمتابعة الحلّ..
وبنفس ما مرّ معنا مع العدد 3 و العدد 2، سنسأل في الدالّة "factorial (1)"، هل العدد 1 أصغر من 1؟
هذه المرّة لن يكون الشرط صحيحًا، ومن ثمّ فسوف تُرجِع الدالّة "factorial (1)" العدد 1، وذلك بناءً على التعليمة الموجودة في السطر رقم 23.. ولكن، ستُرجِع العدد 1 إلى أين؟!
هذه المرّة لن يكون الشرط صحيحًا، ومن ثمّ فسوف تُرجِع الدالّة "factorial (1)" العدد 1، وذلك بناءً على التعليمة الموجودة في السطر رقم 23.. ولكن، ستُرجِع العدد 1 إلى أين؟!
إلى الدالّة "factorial (2)" التي أشرنا إلى أنّها توقّفت مؤقّتًا على العمل بانتظار ناتج الدالّة "factorial (1)"، وها قد عادت الدالّة بالعدد 1، وهنا سيتم إيجاد ناتج الضرب كالتالي:
2 * factorial (1) = 2 * 1 = 2
إذن، فناتج الدالّة "factorial (2)" هو 2 ..
2 * factorial (1) = 2 * 1 = 2
إذن، فناتج الدالّة "factorial (2)" هو 2 ..
وهذا العدد هو ما سوف تُرجِعه الدالّة "factorial (2)" بدورها إلى الدالّة "factorial (3)"، التي توقّفت عن العمل مؤقّتًا هي الأخرى حتى تعود الدالّة "factorial (2)" بالنتيجة التي ستُضرَب في العدد 3، فيكون الناتج كالتالي:
3 * factorial (2) = 3 * 2 = 6
3 * factorial (2) = 3 * 2 = 6
وأخيرًا توصّلَت الدالّة إلى نتيجة مضروب العدد 3، ألا وهو العدد 6، وهكذا تنتهي مهمّتها بنجاح..
بقي أن أنوّه على أمور مهمة، وهي:
بقي أن أنوّه على أمور مهمة، وهي:
أوّلًا: لا بدّ من وجود شرط داخل الدالّة ذاتيّة الاستدعاء (recursive function)، وذلك لمنع تكرار استدعاء الدالّة لنفسها إلى ما لا نهاية، وهذا الشرط يُدعى عادةً "base case" أو "base condition".
ثانيًا: المثال المذكور في هذه السلسلة هو واحد من عدّة استخدامات للدالّة ذاتيّة الاستدعاء (recursive function)، والدالّة ذاتيّة الاستدعاء بمختلف أشكالها هي تجسيد للجانب التطبيقي من الخوارزميّة ذاتيّة الاستدعاء (recursive algorithm).
ثالثًا: من الجدير بالملاحظة، هو أنّ الخوارزميّة ذاتيّة الاستدعاء (recursive algorithm) تطبّق منهجيّة المكدّس (stack) المعروفة في هياكل البيانات (data structure)، بحيث يكون الداخل أخيرًا هو الخارج أوّلًا (LIFO : Last In First Out).. بعبارة أوضح..
آخِر استدعاء للدالّة سيتم حلّه (ستظهر مخرجاته) أوّلًا، ثم الآخِر فالآخِر، وهكذا دواليك.
في النهاية، أتمنّى أن يكون المحتوى بالوضوح المرجو منه، وأن يعود على القارئ بالنفع.
انتهى.
في النهاية، أتمنّى أن يكون المحتوى بالوضوح المرجو منه، وأن يعود على القارئ بالنفع.
انتهى.
جاري تحميل الاقتراحات...