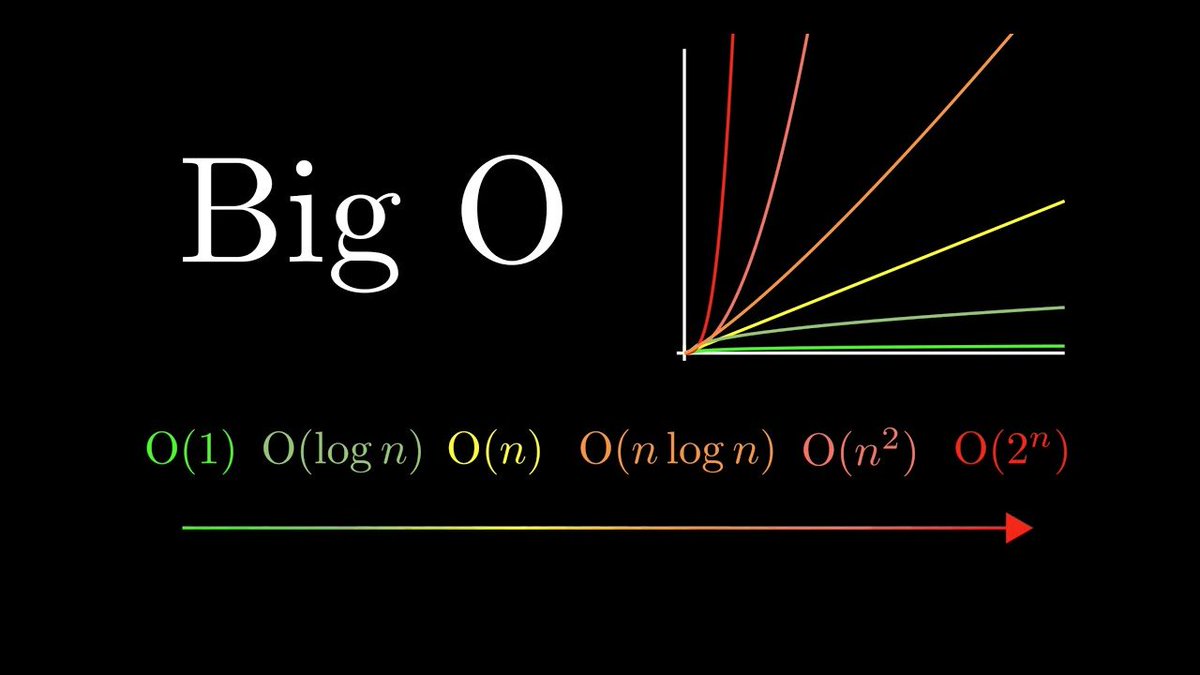❗️ثريدات مهمة لطلبة تقنية المعلومات وعلوم الحاسب❗️
موضوع اليوم:
Big-O notation
ما هي؟ وكيف يتم حسابها؟
موضوع اليوم:
Big-O notation
ما هي؟ وكيف يتم حسابها؟
إذا كنت قد درست بعض المواضيع التدريبية المتعلقة بالخوارزمية، فربما تكون قد سمعت بمصطلح تدوين Big O
إذا لم تقم بذلك، فسنراجعها هنا ، ومن ثم نحصل على فهم أعمق لما هو عليه بالفعل
إذا لم تقم بذلك، فسنراجعها هنا ، ومن ثم نحصل على فهم أعمق لما هو عليه بالفعل
♦️ في البداية علينا تعريف فكرة big-O notation:
تدوين Big O هو تدوين رياضي يصف السلوك المحدود لدالة ما عندما تميل الحجة نحو قيمة معينة أو ما لا نهاية
بكلمات واضحة، يصف تدوين Big O تعقيد الكود الخاص بك باستخدام مصطلحات جبرية
تدوين Big O هو تدوين رياضي يصف السلوك المحدود لدالة ما عندما تميل الحجة نحو قيمة معينة أو ما لا نهاية
بكلمات واضحة، يصف تدوين Big O تعقيد الكود الخاص بك باستخدام مصطلحات جبرية
لفهم ماهية تدوين Big O، يمكننا إلقاء نظرة على مثال نموذجي ، O (n²) ، والذي يُنطق عادةً "Big O squared"، يمثل الحرف "n" هنا حجم الإدخال
- هناك دالّتان: f (n) و g (n) و
f (n) هي f (g (n))
- هناك دالّتان: f (n) و g (n) و
f (n) هي f (g (n))
♦️مثال لحساب وقت خوازمية:
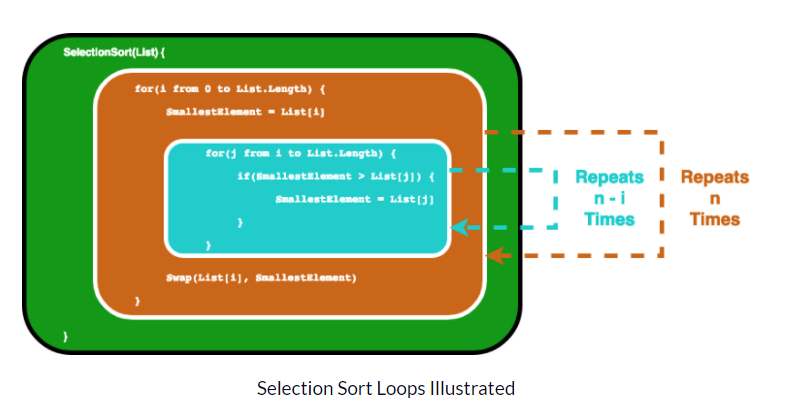
ستكون الخوارزمية النموذجية التي تحتوي على تعقيد O (n²) هي خوارزمية فرز التحديد selection sort
فرز التحديد هو خوارزمية فرز تتكرر عبر القائمة للتأكد من أن كل عنصر في الفهرس i هو أصغر / أكبر عنصر في القائمة
ستكون الخوارزمية النموذجية التي تحتوي على تعقيد O (n²) هي خوارزمية فرز التحديد selection sort
فرز التحديد هو خوارزمية فرز تتكرر عبر القائمة للتأكد من أن كل عنصر في الفهرس i هو أصغر / أكبر عنصر في القائمة
يمكن وصف الخوارزمية من خلال الكود في الصورة
للتأكد من أن العنصر i هو أصغر عنصر في القائمة، تتكرر هذه الخوارزمية أولاً عبر القائمة باستخدام حلقة for
ثم يستخدم كل عنصر حلقة for أخرى للعثور على أصغر عنصر في الجزء المتبقي من القائمة
للتأكد من أن العنصر i هو أصغر عنصر في القائمة، تتكرر هذه الخوارزمية أولاً عبر القائمة باستخدام حلقة for
ثم يستخدم كل عنصر حلقة for أخرى للعثور على أصغر عنصر في الجزء المتبقي من القائمة
في هذا السيناريو، نعتبر القائمة المتغيرة هي المدخلات، وبالتالي فإن حجم الإدخال n هو عدد العناصر داخل القائمة
افترض أن عبارة if وتعيين القيمة المقيدة بعبارة if تستغرق وقتًا ثابتًا
ثم يمكننا العثور على رمز O الكبير للدالة من خلال تحليل عدد المرات التي يتم فيها تنفيذ التعليمات
افترض أن عبارة if وتعيين القيمة المقيدة بعبارة if تستغرق وقتًا ثابتًا
ثم يمكننا العثور على رمز O الكبير للدالة من خلال تحليل عدد المرات التي يتم فيها تنفيذ التعليمات
أولاً تقوم حلقة for الداخلية بتشغيل العبارات داخل n من المرات
وبعد زيادة i، يتم تشغيل حلقة for الداخلية لـ n-1 مرة حتى يتم تشغيلها مرة واحدة ، ثم تصل كلتا الحلقتين for إلى شروط الإنهاء الخاصة بهما
وبعد زيادة i، يتم تشغيل حلقة for الداخلية لـ n-1 مرة حتى يتم تشغيلها مرة واحدة ، ثم تصل كلتا الحلقتين for إلى شروط الإنهاء الخاصة بهما
ينتهي هذا الأمر في الواقع بإعطائنا مجموعًا هندسيًا ، ومع بعض الرياضيات سنجد أن الحلقة الداخلية ستتكرر لمدة 1 + 2 ... + n مرة ، والتي تساوي n (n-1) / 2 مرة
إذا ضربنا هذا ، فسنحصل في النهاية على (n² / 2) - (n / 2)
إذا ضربنا هذا ، فسنحصل في النهاية على (n² / 2) - (n / 2)
عندما نحسب تدوين O، فإننا نهتم فقط بالمصطلحات السائدة، ولا نهتم بالمعاملات
وهكذا نأخذ n² على أنها O الأخيرة الكبيرة لدينا، نكتبها كـ
O (n²) ، والتي تُنطق مرة أخرى "Big O تربيع".
وهكذا نأخذ n² على أنها O الأخيرة الكبيرة لدينا، نكتبها كـ
O (n²) ، والتي تُنطق مرة أخرى "Big O تربيع".
♦️سبعة انواع يمكن ان تكون نتيجة لO:
1- Constant = 1
2- Logarithmic = log n
3- Linear = n
4- N-log-n = n log n
5- Quadratic = n^2
6- Cubic = n^3
7- Exponential = 2^n
1- Constant = 1
2- Logarithmic = log n
3- Linear = n
4- N-log-n = n log n
5- Quadratic = n^2
6- Cubic = n^3
7- Exponential = 2^n
♦️مثال لكيفية حساب الوقت المعقد لحلقة for:
تأخذ هذه الحلقة K * n حيث K هي المدة التي تستغرقها حلقة واحدة و n هي عدد المرات خلال الحلقة
إذن إجمالي الوقت هو K * n وهو خطي: O (n)
تأخذ هذه الحلقة K * n حيث K هي المدة التي تستغرقها حلقة واحدة و n هي عدد المرات خلال الحلقة
إذن إجمالي الوقت هو K * n وهو خطي: O (n)
♦️خطوات حساب big O :
لحساب Big O ، هناك خمس خطوات يجب عليك اتباعها:
1- قسّم الخوارزمية / الدالّة إلى عمليات فردية
2- احسب O الكبير لكل عملية
3- أضف Big O لكل عملية معًا
4- احذف الثوابت
5- ابحث عن المصطلح الأعلى رتبة، سيكون هذا ما نعتبره Big O لخوارزمية / وظيفة لدينا
لحساب Big O ، هناك خمس خطوات يجب عليك اتباعها:
1- قسّم الخوارزمية / الدالّة إلى عمليات فردية
2- احسب O الكبير لكل عملية
3- أضف Big O لكل عملية معًا
4- احذف الثوابت
5- ابحث عن المصطلح الأعلى رتبة، سيكون هذا ما نعتبره Big O لخوارزمية / وظيفة لدينا
♦️O (1) لديه أقل تعقيد:
غالبًا ما يُطلق عليه "الوقت الثابت" ، إذا كان بإمكانك إنشاء خوارزمية لحل المشكلة في O (1)، فأنت على الأرجح في أفضل حالاتك
في بعض السيناريوهات، قد يتجاوز التعقيد O (1)، ثم يمكننا تحليلها من خلال إيجاد نظيره O (1 / g (n))
غالبًا ما يُطلق عليه "الوقت الثابت" ، إذا كان بإمكانك إنشاء خوارزمية لحل المشكلة في O (1)، فأنت على الأرجح في أفضل حالاتك
في بعض السيناريوهات، قد يتجاوز التعقيد O (1)، ثم يمكننا تحليلها من خلال إيجاد نظيره O (1 / g (n))
هل تعلمت شيئ جديد؟ لا تنس اعادة التغريد حتى يستفيد الجميع🙏
جاري تحميل الاقتراحات...