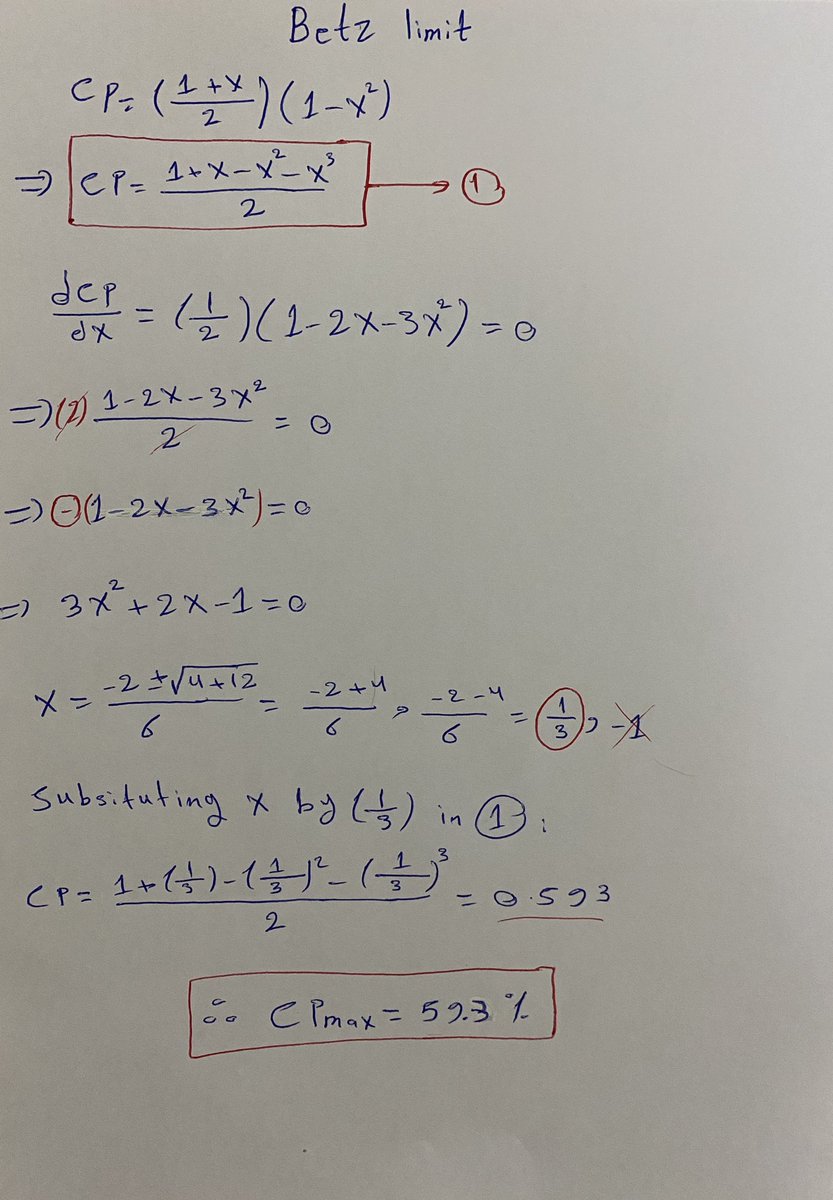أحد أشهر ما توصل إليه ألبرت بيتز أنه أقصى كفاءة لطاقة الرياح التي ستتحول إلى طاقة كهربائية هي 59.3% ولا يمكن أن تزيد عن ذلك، ولكن كيف استنتج ذلك؟ وكيف توصل إلى هذه النسبة تحديدا؟
تابعوا معي لمعرفة وفهم ذلك.
#هندسة_كهربائية
@Electric_Engg
تابعوا معي لمعرفة وفهم ذلك.
#هندسة_كهربائية
@Electric_Engg
يفضل مراجعة هذين الثريدين لفهم واستيعاب الموضوع 👇🏻
1- P(Wind)
2- P(Electrical)
1- P(Wind)
2- P(Electrical)
قبل أن نبدأ دعونا نستذكر معادلة Cp التي توصلنا إليها في ثريد سابق وهي كالآتي :
Cp=((1+x)/2)(1-x^2)
<<
Cp=(1+x-x^2-x^3)/2
لمعرفة كيف توصلنا إلى معادلة Cp :
Cp=((1+x)/2)(1-x^2)
<<
Cp=(1+x-x^2-x^3)/2
لمعرفة كيف توصلنا إلى معادلة Cp :
رياضيا إذا أردنا أن نستخرج النقطة التي تكون عندها القيمة القصوى للدالة يتم اشتقاقها بالنسبة لمحور x ومن ثم مساواتها بالصفر، وهذا بالضبط ما سنفعله مع معادلة Cp حيث سيتم أولا اشتقاقها لتصبح كالآتي :
dCp/dx=(0+1-2x-3x^2)/2
dCp/dx=(0+1-2x-3x^2)/2
والآن بعد أن تم اشتقاقها سنساويها بالصفر وفي نفس الوقت نضرب الطرفين في ٢ للتخلص من (1/2) لتصبح كالآتي :
1-2x-3x^2)=0)
وبضرب الطرفين في سالب تصبح كالآتي :
3x^2+2x-1=0
معادلة من الدرجة الثانية تحل بكل سهولة ، وبعد حلها سنجد أنه الناتج عبارة عن حلين وهما -1 و 1/3 فأيهما سنأخذ؟؟
1-2x-3x^2)=0)
وبضرب الطرفين في سالب تصبح كالآتي :
3x^2+2x-1=0
معادلة من الدرجة الثانية تحل بكل سهولة ، وبعد حلها سنجد أنه الناتج عبارة عن حلين وهما -1 و 1/3 فأيهما سنأخذ؟؟
رياضيا كلا الحلين صحيحين، لكن بالمنطق الفيزيائي -1 ليست حل منطقي، لأنه من المستحيل أن تكون السرعة بالسالب، لذا 1/3 هو الحل الصحيح والمنطقي.
والآن نعود لمعادلة Cp ونعوض كل (x) ب (1/3) لتصبح كالآتي :
Cp=((1+(1/3))/2)(1-(1/3)^2)=0.593
وبذلك توصلنا إلى النسبة التي توصل إليها بيتز وهي 59.3%، وملخص كل ما ذكرناه بالصورة أدناه.
انتهى
@rattibha
Cp=((1+(1/3))/2)(1-(1/3)^2)=0.593
وبذلك توصلنا إلى النسبة التي توصل إليها بيتز وهي 59.3%، وملخص كل ما ذكرناه بالصورة أدناه.
انتهى
@rattibha
جاري تحميل الاقتراحات...