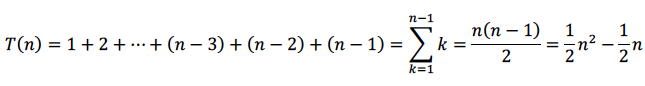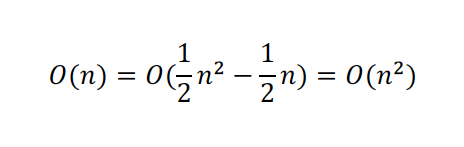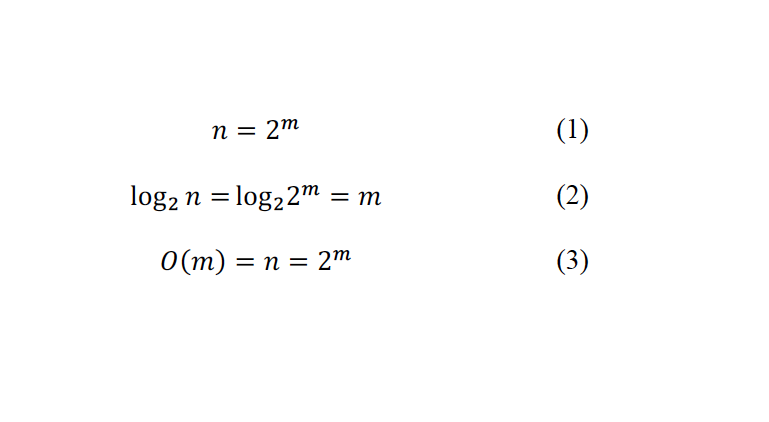#خوارزميون
@PrograminLovers
مقدمة في أساسيات تصميم الخوارزميات – خوارزميات القوة الغاشمة:
في هذه السلسلة أتحدث عن أحد أساليب تصميم الخوارزميات وهو ما يعرف بالقوة الغاشمة (Brute force)
@PrograminLovers
مقدمة في أساسيات تصميم الخوارزميات – خوارزميات القوة الغاشمة:
في هذه السلسلة أتحدث عن أحد أساليب تصميم الخوارزميات وهو ما يعرف بالقوة الغاشمة (Brute force)
تتميز عملية تحليل الخوارزميات بآلية واضحة ومحددة لتحديد الكفاءة كدالة في حجم المدخلات. وفي المقابل لا توجد آلية ثابتة لتصميم الخوارزميات، وإنما يعتمد التصميم على نوع المشكلة، وقدرة المصمم على توظيف أساليب التصميم المشهورة، أو ابتكار تصاميم ذكية للحصول على أفضل كفاءة للخوارزمية
وفيما يلي أعرض أشهر أساليب تصميم الخوارزميات. ويلاحظ أن هذه الأساليب تم تسميتها بمسميات لا تخلو من الطرافة، ولكنها تعبر بشكل كبير عن آلية عمل الخوارزميات
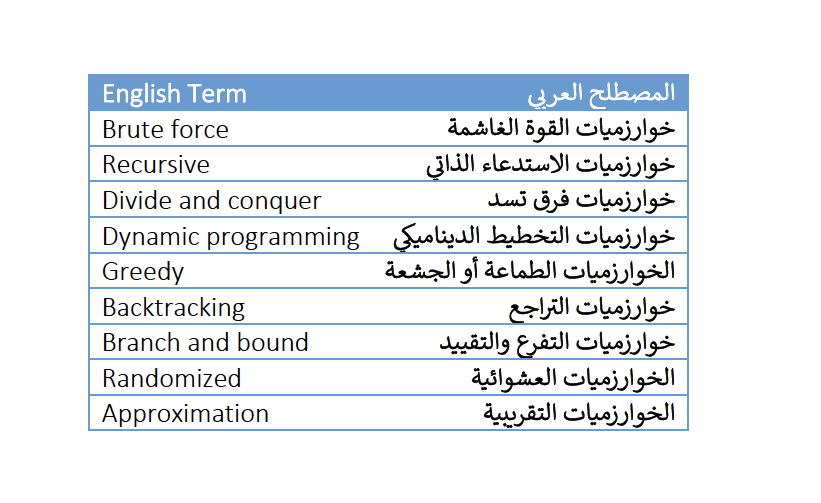
١ خوارزميات القوة الغاشمة
٢ خوارزميات الاستدعاء الذاتي
٣ خوارزميات فرق تسد
٤ خوارزميات التخطيط الديناميكي
٥ الخوارزميات الطماعة أو الجشعة
٦ خوارزميات التراجع
٧ خوارزميات التفرع والتقييد
٨ الخوارزميات العشوائية
٩ الخوارزميات التقريبية
٢ خوارزميات الاستدعاء الذاتي
٣ خوارزميات فرق تسد
٤ خوارزميات التخطيط الديناميكي
٥ الخوارزميات الطماعة أو الجشعة
٦ خوارزميات التراجع
٧ خوارزميات التفرع والتقييد
٨ الخوارزميات العشوائية
٩ الخوارزميات التقريبية
هنا أتحدث عن النوع الأول وهو خوارزميات القوة الغاشمة. وهذا النوع يحاول حل المشكلة بطريقة مباشرة ويكون التركيز على إيجاد حل للمشكلة بغض النظر عن التكاليف (الوقت/المساحة). عادة تعتمد هذه الطريقة على تجربة جميع الاحتمالات الممكنة، وبالتالي نادرا ما ينتج عنها خوارزميات ذكية أو فعالة
وفيما يلي أستعرض بعض الأمثلة لهذا النوع من الخوارزميات لتوضيح طريقة عملها، وتحديد متى تعتبر ناجحة ومتى تكون فاشلة.
خوارزمية إيجاد العنصر الأصغر: المشكلة المطلوب حلها هي إيجاد العنصر الأصغر في مصفوفة مكونة من (n) من العناصر.
خوارزمية إيجاد العنصر الأصغر: المشكلة المطلوب حلها هي إيجاد العنصر الأصغر في مصفوفة مكونة من (n) من العناصر.
حل المشكلة بأسلوب القوة الغاشمة:
نبدأ من العنصر الأول ونعتبره العنصر الأصغر (MinVal)، ثم نمر على بقية العناصر ونقارن كل عنصر بالعنصر الأصغر (MinVal)، وفي حال كان العنصر الحالي أصغر من (MinVal)، نعتبره هو العنصر الأصغر (MinVal). تستمر العملية حتى يتم الانتهاء من جميع العناصر
نبدأ من العنصر الأول ونعتبره العنصر الأصغر (MinVal)، ثم نمر على بقية العناصر ونقارن كل عنصر بالعنصر الأصغر (MinVal)، وفي حال كان العنصر الحالي أصغر من (MinVal)، نعتبره هو العنصر الأصغر (MinVal). تستمر العملية حتى يتم الانتهاء من جميع العناصر
تحليل كفاءة الخوارزمية:
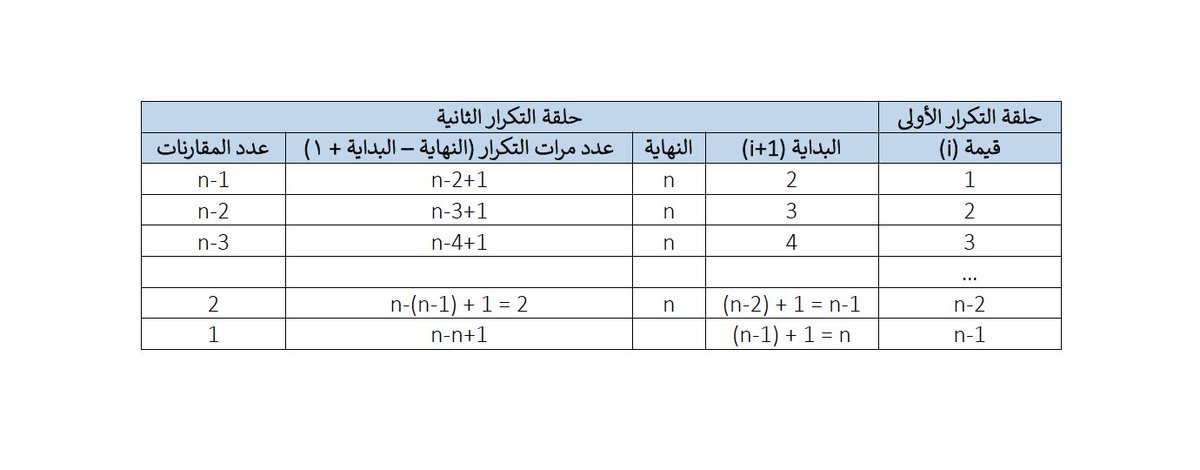
كما مر معنا سابقا فإن كفاءة الوقت لهذه الخوارزمية هي
O(n) = n
كما مر معنا سابقا فإن كفاءة الوقت لهذه الخوارزمية هي
O(n) = n
ما مدى فعالية القوة الغاشمة في حل المشكلة؟
لتقييم فعالية أسلوب القوة الغاشمة في حل هذه المشكلة نقارن كفاءة الخوارزمية مع فئات الكفاءة الأساسية.
* كفاءة هذه الخوارزمية تقع ضمن الفئة الخطية O(n)=n،
* وهناك فئتين أكثر كفاءة وهما
اللوغارتمية O(n)=log n
والثابتة O(n)=1
لتقييم فعالية أسلوب القوة الغاشمة في حل هذه المشكلة نقارن كفاءة الخوارزمية مع فئات الكفاءة الأساسية.
* كفاءة هذه الخوارزمية تقع ضمن الفئة الخطية O(n)=n،
* وهناك فئتين أكثر كفاءة وهما
اللوغارتمية O(n)=log n
والثابتة O(n)=1
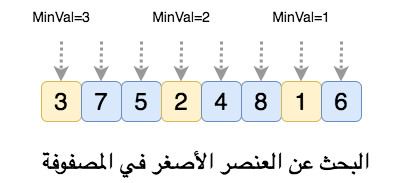
* هل يمكن التوصل إلى حل لهذه المشكلة ضمن هاتين الفئتين؟
* الجواب نعم يمكن حلها في وقت ثابت O(n)=1، ولكن بشرط أن تكون المصفوفة مرتبة من الأصغر إلى الأعلى، وعندها نستطيع إيجاد العنصر الأصغر من خلال اختيار العنصر الأول في المصفوفة
* الجواب نعم يمكن حلها في وقت ثابت O(n)=1، ولكن بشرط أن تكون المصفوفة مرتبة من الأصغر إلى الأعلى، وعندها نستطيع إيجاد العنصر الأصغر من خلال اختيار العنصر الأول في المصفوفة
* لكن هذا الحل يتطلب ترتيب المصفوفة أولا، وأفضل كفاءة ممكنة لخوارزميات الترتيب هي O(n)=n log n كما سنرى لا حقا بإذن الله
* بالتالي يمكن اعتبار أسلوب القوة الغاشمة هو الحل الأفضل لهذه المشكلة
* بالتالي يمكن اعتبار أسلوب القوة الغاشمة هو الحل الأفضل لهذه المشكلة
خوارزمية الترتيب بالاختيار (Selection Sort): المشكلة المطلوب حلها هي ترتيب عناصر مصفوفة مكونة من (n) من العناصر تصاعديا من الأصغر إلى الأعلى
حل المشكلة بأسلوب القوة الغاشمة:
نبدأ بالمرور على عناصر المصفوفة كاملة للعثور على أصغر عنصر واستبداله بالعنصر الأول، ثم نعيد العملية ابتداء من العنصر الثاني للعثور على العنصر الأصغر بين العناصر المتبقية (n-1) واستبداله بالعنصر الثاني، وتستمر هذه العملية حتى يتم ترتيب المصفوفة.
نبدأ بالمرور على عناصر المصفوفة كاملة للعثور على أصغر عنصر واستبداله بالعنصر الأول، ثم نعيد العملية ابتداء من العنصر الثاني للعثور على العنصر الأصغر بين العناصر المتبقية (n-1) واستبداله بالعنصر الثاني، وتستمر هذه العملية حتى يتم ترتيب المصفوفة.
تحليل كفاءة الخوارزمية:
* نبدأ بتحديد العملية الأساسية الأكثر تكرارا وهي عملية المقارنة في السطر ٤
* نحسب عدد مرات تكرار هذه العملية كما في الجدول
الخطوة الأولى (i=1) عدد المقارنات (n-1)
الخطوة الثانية (i=2) عدد المقارنات (n-2)
...
الخطوة الأخيرة (i=n-1) عدد المقارنات ١
* نبدأ بتحديد العملية الأساسية الأكثر تكرارا وهي عملية المقارنة في السطر ٤
* نحسب عدد مرات تكرار هذه العملية كما في الجدول
الخطوة الأولى (i=1) عدد المقارنات (n-1)
الخطوة الثانية (i=2) عدد المقارنات (n-2)
...
الخطوة الأخيرة (i=n-1) عدد المقارنات ١
* نقوم بإيجاد مجموع المقارنات في جميع هذه الخطوات من العمود الأخير في الجدول
ملاحظة: يمكن حساب سلسلة الجمع باستخدام الآلة الحاسبة أو جداول سلاسل الجمع أو باستخدام مواقع مثل (WolframAlpha)
ملاحظة: يمكن حساب سلسلة الجمع باستخدام الآلة الحاسبة أو جداول سلاسل الجمع أو باستخدام مواقع مثل (WolframAlpha)
* أخيرا نحسب معدل النمو لوقت الخوارزمية بناء على عدد مرات التكرار وهو:
ما مدى فعالية أسلوب القوة الغاشمة في حل هذه المشكلة؟
لتقييم فعالية أسلوب القوة الغاشمة في حل هذه المشكلة نقارن كفاءة الخوارزمية مع فئات الكفاءة الأساسية.
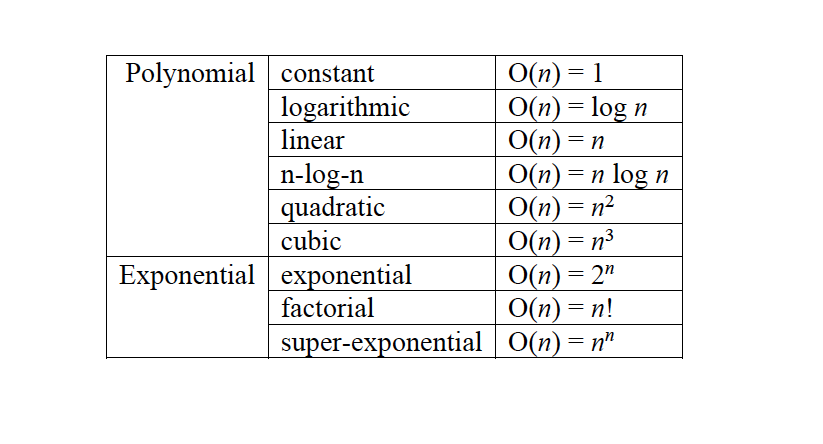
* كفاءة هذه الخوارزمية تقع ضمن فئة الدرجة الثانية
* هناك ٤ فئات أكثر كفاءة من هذه الفئة
لتقييم فعالية أسلوب القوة الغاشمة في حل هذه المشكلة نقارن كفاءة الخوارزمية مع فئات الكفاءة الأساسية.
* كفاءة هذه الخوارزمية تقع ضمن فئة الدرجة الثانية
* هناك ٤ فئات أكثر كفاءة من هذه الفئة
* هل يمكن التوصل إلى حل لهذه المشكلة ضمن هذه الفئات؟
* الجواب نعم يوجد خوارزميات لحل هذه المشكلة في وقت
O(n)=n log n
باستخدام أساليب أخرى لتصميم الخوارزميات كما سيمر معنا لاحقا
* بالتالي نستنتج أن أسلوب القوة الغاشمة ليس هو الحل الأفضل لهذه المشكلة
* الجواب نعم يوجد خوارزميات لحل هذه المشكلة في وقت
O(n)=n log n
باستخدام أساليب أخرى لتصميم الخوارزميات كما سيمر معنا لاحقا
* بالتالي نستنتج أن أسلوب القوة الغاشمة ليس هو الحل الأفضل لهذه المشكلة
خوارزمية حساب الأس: المشكلة المطلوب حلها هي إيجاد قيمة العدد (a) مرفوعا للأس (n)
حل المشكلة بأسلوب القوة الغاشمة:
الطريقة المباشرة لحل هذه المشكلة هي بضرب العدد (a) في نفسه (n) من المرات.
حل المشكلة بأسلوب القوة الغاشمة:
الطريقة المباشرة لحل هذه المشكلة هي بضرب العدد (a) في نفسه (n) من المرات.
تحليل كفاءة الخوارزمية:
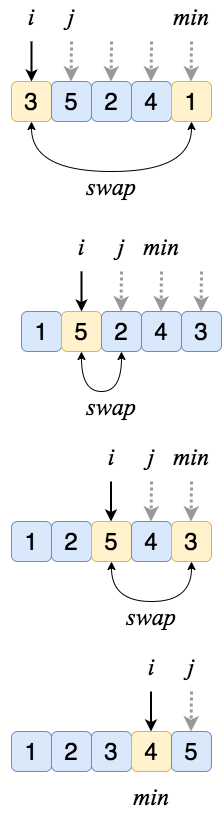
* العملية الأساسية الأكثر تكرارا هي عملية الضرب في السطر ٣
* نحسب عدد مرات تكرار هذه العملية وهو (n) فتكون كفاءة هذه الخوارزمية
O(n) = n
* ولكن كفاءة الخوارزميات تحسب كدالة في حجم المدخلات، وحيث أن (n) هو عدد واحد وليس مصفوفة، فإن حجمه يقاس بعدد البت
* العملية الأساسية الأكثر تكرارا هي عملية الضرب في السطر ٣
* نحسب عدد مرات تكرار هذه العملية وهو (n) فتكون كفاءة هذه الخوارزمية
O(n) = n
* ولكن كفاءة الخوارزميات تحسب كدالة في حجم المدخلات، وحيث أن (n) هو عدد واحد وليس مصفوفة، فإن حجمه يقاس بعدد البت
* لتسهيل عمليات الحساب نفترض أن العدد (n) هو أحد قوى العدد ٢ (مثلا ٢، ٤، ٨، ...)، وبالتالي يمكن تمثيله كما في المعادلة ١:
* وبالتالي يمكن حساب عدد البت (m) الموجودة في العدد (n) كما المعادلة ٢:
* والآن نحسب كفاءة الخوارزمية كدالة في حجم المدخلات (m) كما في المعادلة ٣:
* وبالتالي يمكن حساب عدد البت (m) الموجودة في العدد (n) كما المعادلة ٢:
* والآن نحسب كفاءة الخوارزمية كدالة في حجم المدخلات (m) كما في المعادلة ٣:
ما مدى فعالية أسلوب القوة الغاشمة في حل المشكلة؟
لتقييم فعالية أسلوب القوة الغاشمة نقارن كفاءة الخوارزمية مع فئات الكفاءة الأساسية
* كفاءة الخوارزمية تقع ضمن الفئة الأسية وهي غير عملية إطلاقا مع زيادة حجم المدخلات (m)
*هل يمكن التوصل إلى حل لهذه المشكلة ضمن الفئات الأقل تعقيدا؟
لتقييم فعالية أسلوب القوة الغاشمة نقارن كفاءة الخوارزمية مع فئات الكفاءة الأساسية
* كفاءة الخوارزمية تقع ضمن الفئة الأسية وهي غير عملية إطلاقا مع زيادة حجم المدخلات (m)
*هل يمكن التوصل إلى حل لهذه المشكلة ضمن الفئات الأقل تعقيدا؟
* الجواب نعم، ولكن الحل يتطلب تصميم خوارزمية أكثر ذكاء باستخدام التخطيط الديناميكي، الذي سيتم شرحه مستقبلا بإذن الله.
* كفاءة الطريقة الثانية هي (log n)، وهي أفضل من القوة الغاشمة
vimeo.com
* كفاءة الطريقة الثانية هي (log n)، وهي أفضل من القوة الغاشمة
vimeo.com
على الرغم من أنه نادرا ما يكون أسلوب القوة الغاشمة مصدرا للخوارزميات الذكية أو الفعالة، لكن لا ينبغي التغاضي عن هذا الأسلوب كاستراتيجية مهمة لتصميم الخوارزميات وذلك للأسباب التالية
١ على عكس الاستراتيجيات الأخرى، فإن القوة الغاشمة قابلة للتطبيق تقريبا على جميع المشكلات
١ على عكس الاستراتيجيات الأخرى، فإن القوة الغاشمة قابلة للتطبيق تقريبا على جميع المشكلات
٢ بالنسبة لبعض المشكلات (الترتيب والبحث وضرب المصفوفات) ينتج عن القوة الغاشمة خوارزميات بكفاءة عملية مقبولة
٣ تعتبر خوارزميات القوة الغاشمة مفيدة في حل الحالات صغيرة الحجم
٤ تخدم خوارزميات القوة الغاشمة كمقياس يمكن من خلاله الحكم على بدائل أكثر كفاءة لحل المشكلة
٣ تعتبر خوارزميات القوة الغاشمة مفيدة في حل الحالات صغيرة الحجم
٤ تخدم خوارزميات القوة الغاشمة كمقياس يمكن من خلاله الحكم على بدائل أكثر كفاءة لحل المشكلة
جاري تحميل الاقتراحات...