رتبها

#خوارزميون
@PrograminLovers
مقدمة في أساسيات تحليل الخوارزميات – الجزء الثاني
في هذه الجزء أستكمل الحديث عن أساسيات تحليل الخوارزميات، من خلال شرح القسمين الرئيسيين لتحليل الخوارزميات وهما:
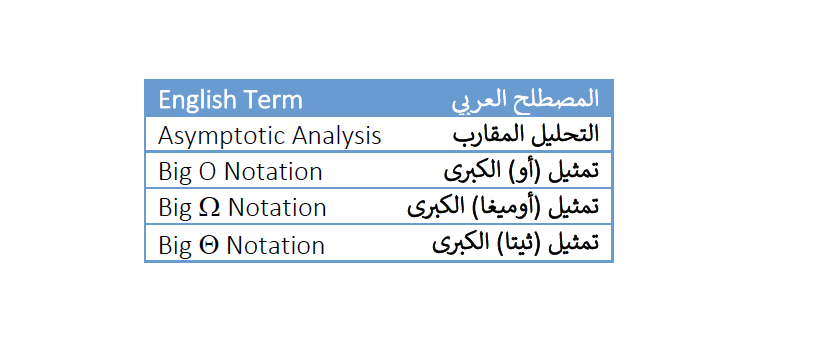
١- التحليل المقارب
٢- التحليل التجريبي

التحليل المقارب
هو تحليل رياضي لكفاءة الخوارزميات باستخدام معدل النمو، ويتكون من ثلاثة دوال (O, Ω, Θ) تمثل الحد الأعلى والحد الأدني لوقت تنفيذ الخوارزمية.

هنا لن أتكلم عن التعريف الرياضي لهذه الدوال، ولكن سأكتفي بشرح المفهوم العام لها، وطريقة استخدامها في تحليل الخوارزميات من خلال بعض الأمثلة البسيطة.
تمثيل (أو) الكبرى: يتم استخدامه للتعبير عن الحد الأعلى للخوارزمية والذي يعطي المقياس لأطول وقت قد تستغرقه الخوارزمية حتى تكتمل.

تمثيل (أوميغا) الكبرى: يتم استخدامه للتعبير عن أفضل قدر من الوقت يمكن أن تستغرقه الخوارزمية حتى تكتمل.
تمثيل (ثيتا) الكبرى: يتم استخدامه للتعبير عن كل من الحد الأدنى والحد الأعلى للوقت الذي يمكن أن تستغرقه الخوارزمية حتى تكتمل. وتكون هذه الدالة موجودة فقط في حال كانت
O(n) = Ω(n)

مثال ١: خوارزمية البحث الخطي. هذه الخوارزمية تبحث عن عنصر (x) في مصفوفة مكونة من (n) من العناصر. وتقوم الخوارزمية بإعادة موقع أول عنصر في المصفوفة يطابق العنصر (x)، أو تقوم بإعادة صفر في حال لم يتم إيجاد (x) في المصفوفة.

يتم التحليل المقارب للخوارزمية في ٤ خطوات:
١ تحديد العملية الأساسية في هذه الخوارزمية: يوجد عمليتين أساسيتين في السطر ٢ كلاهما عملية مقارنة، يمكن أن نختار أي واحدة منهما لتكون هي العملية الأساسية.

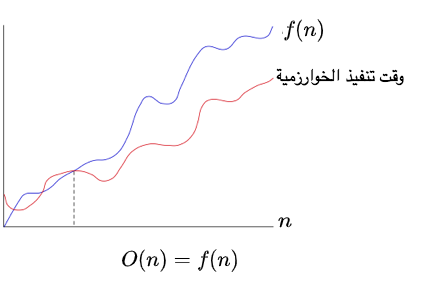
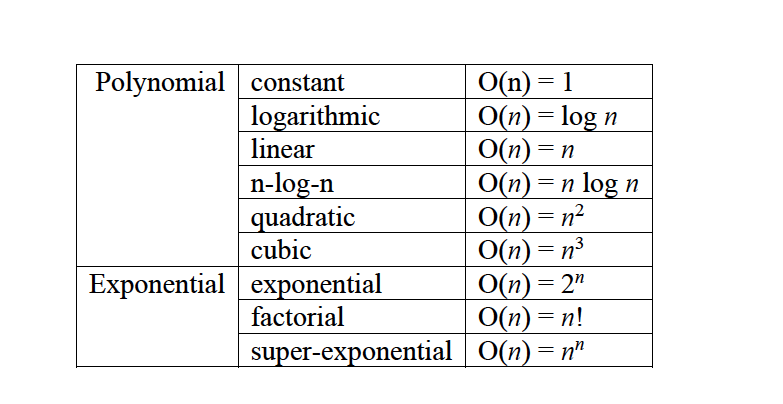
٢ تحديد الحد الأعلى لمرات تنفيذ العملية الأساسية: عملية المقارنة تستمر حتى نجد أول مطابقة للعنصر (x) أو حتى نصل إلى العنصر الأخير، وبالتالي يكون أقصى عدد للمقارنات هو (n). إذا وقت التنفيذ الأعلى للخوارزمية هو T(n)=n. وبناء عليه يكون الحد الأعلى لوقت تنفيذ الخوارزمية هو O(n)=n

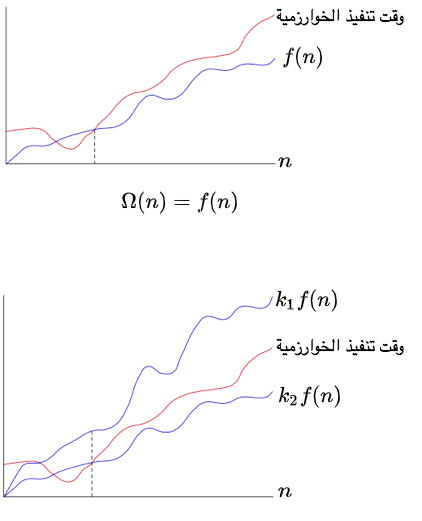
٣ تحديد الحد الأدنى لمرات تنفيذ العملية الأساسية: عملية المقارنة تحدث مرة واحدة فقط في حال كان العنصر (x) مطابقا للعنصر الأول في المصفوفة. وبالتالي يكون وقت التنفيذ الأدنى للخوارزمية هو T(n)=1. وبناء عليه الحد الأدنى لوقت تنفيذ الخوارزمية هو Ω(n)=1

٤ مقارنة الحد الأدنى والحد الأعلى: بمقارنة الحد الأعلى والحد الأدنى نجد أن (Ω(n)≠O(n وبالتالي تكون (Θ(n غير معرفة. وبالتالي يكون أداء هذه الخوارزمية متفاوتا حسب قيمة العنصر (x) ولا يعتمد فقط على حجم المصفوفة (n).

مثال ٢: خوارزمية إيجاد العدد الأصغر في مصفوفة مكونة من (n) من العناصر
التحليل المقارب للخوارزمية:
١ تحديد العملية الأساسية في هذه الخوارزمية: العملية الأساسية في هذه الخوارزمية هي عملية المقارنة في السطر ٣.

٢ تحديد الحد الأعلى لمرات تنفيذ العملية الأساسية: العملية الأساسية يتم تكرارها (n-1) من المرات لأن حلقة التكرار يتم تنفيذها من (2) إلى (n). وبالتالي يكون أقصى عدد للمقارنات هو (n-1).

وبالتالي يكون وقت التنفيذ الأعلى هو T(n)=n-1. وبناء عليه يكون الحد الأعلى لوقت تنفيذ الخوارزمية هو O(n)=n. لاحظ أنه تم الاستغناء عن الحد الثابت (-1) لأنه لا يؤثر على معدل النمو للخوارزمية كما تم توضيحه في الجزء الأول

٣ تحديد الحد الأدنى لمرات تنفيذ العملية الأساسية: هذه الخوارزمية تحتاج المرور على جميع عناصر المصفوفة بدون استثناء لتحديد العنصر الأصغر. وبالتالي يكون وقت التنفيذ الأدنى للخوارزمية مساويا لوقت التنفيذ الأعلى. وبناء عليه يكون الحد الأدنى لوقت تنفيذ الخوارزمية هو Ω(n)=n

٤ مقارنة الحد الأدنى والحد الأعلى: بمقارنة الحد الأعلى والحد الأدنى نجد أن (Ω(n)=O(n وبالتالي تكون
Θ(n)=n
وهنا يتبين لنا أن أداء هذه الخوارزمية ثابت ويعتمد فقط على حجم المصفوفة (n)

فئات الكفاءة الأساسية
يوضح الجدول التالي كفاءة الخوارزميات مرتبة من الأفضل إلى الأسوأ. وهذه الفئات مقسمة إلى مجموعتين: الخوارزميات متعددة الحدود والخوارزميات الأسية.

وكما ذكرت سابقا فإن النوع الأول يمكن تنفيذه بشكل عملي لحل المشكلة بوقت معقول، أما النوع الثاني فلا يمكن تنفيذه بشكل عملي لحل المشكلة في وقت معقول، ويتم الاستعاضة عنها بخوارزميات تقريبية للحصول على حلول قريبة من الحل الأمثل للمشكلة.

التحليل التجريبي
يعتبر التحليل التقريبي هو الأداة الأساسية في تحليل الخوارزميات رياضيا، ولكن توجد حالات كثيرة تتطلب إجراء تحليل عملي للخوارزميات بعد تنفيذها برمجيا

ومن هذه الحالات:
* اختبار تنفيذ الخوارزمية على هاردوير معين
* اختبار عوامل أخرى غير وقت التنفيذ مثل نتائج الخوارزمية في حل المشكلة مقارنة بخوارزميات أخرى
* اختبار أداء الخوارزمية نتيجة لتغيير المدخلات ومعاملات الخوارزمية
* اختبار أداء الخوارزمية باستخدام مجموعة اختبار معينة

يتم إجراء التحليل التجريبي للخوارزمية كما يلي:
١ تحديد مقياس الكفاءة المراد قياسه (الوقت، المساحة، نتائج حل المشكلة)
٢ تحدد خصائص عينة المدخلات (نوعها، مداها، حجمها)
٣ كتابة برنامج لتنفيذ الخوارزمية
٤ توليد عينة من المدخلات إما عشوائيا أو باستخدام بيانات اختبار متعارف عليها

٥ تشغيل الخوارزمية على مدخلات العينة وتسجل المخرجات أو النتائج
٦ تحليل البيانات التي تم الحصول عليها أو مقارنتها مع نتائج خوارزميات أخرى
وتوضح الصورة التالية نتائج تحليل تجريبي لبعض خوارزميات الترتيب

التصنيفات

المزيد من هذا الكاتب

مواضيع ذات صلة

الأكثر اعجابا

التصنيفات

المزيد من هذا الكاتب

مواضيع ذات صلة

الأكثر اعجابا

فك الثريد