مقدمة في أساسيات تحليل الخوارزميات - الجزء الأول
في هذه السلسلة أعرض مقدمة لأساسيات تحليل الخوارزميات مع بعض الأمثلة البسيطة وتصحيح لبعض المفاهيم التي قد تفوت على طلبة علوم الحاسب أثناء دراسة هذا العلم.
في هذه السلسلة أعرض مقدمة لأساسيات تحليل الخوارزميات مع بعض الأمثلة البسيطة وتصحيح لبعض المفاهيم التي قد تفوت على طلبة علوم الحاسب أثناء دراسة هذا العلم.
يهدف تحليل الخوارزميات إلى قياس فعالية الخوارزمية باستخدام مقياسين مهمين:
١ - كفاءة الوقت: يشير إلى مدى سرعة الخوارزمية في حل المشكلة
٢ - كفاءة المساحة: يشير إلى مقدار وحدات الذاكرة التي تتطلبها الخوارزمية بدون احتساب المساحة اللازمة للمدخلات والمخرجات.
١ - كفاءة الوقت: يشير إلى مدى سرعة الخوارزمية في حل المشكلة
٢ - كفاءة المساحة: يشير إلى مقدار وحدات الذاكرة التي تتطلبها الخوارزمية بدون احتساب المساحة اللازمة للمدخلات والمخرجات.
قياس حجم المدخلات
الوقت الذي تستغرقه الخوارزمية يعتمد على حجم المدخلات. على سبيل المثال، تستغرق الخوارزميات وقتا أطول لإجراء العمليات (مثل الترتيب، البحث، الضرب، ...) على المصفوفات الأكبر حجما. لذلك، من المنطقي أن يتم حساب كفاءة الخوارزميات كدالة تعتمد على حجم المدخلات (n).
الوقت الذي تستغرقه الخوارزمية يعتمد على حجم المدخلات. على سبيل المثال، تستغرق الخوارزميات وقتا أطول لإجراء العمليات (مثل الترتيب، البحث، الضرب، ...) على المصفوفات الأكبر حجما. لذلك، من المنطقي أن يتم حساب كفاءة الخوارزميات كدالة تعتمد على حجم المدخلات (n).
وفيما يلي أوضح طريقة حساب حجم المدخلات لهياكل البيانات الأكثر استخداما:
* المصفوفة ثنائية الأبعاد (m x n): يكون حجم المدخلات بعدد عناصر المصفوفة (n x m)
* المصفوفة الأحادية (1 x n): يكون حجم المدخلات بعدد عناصر المصفوفة (n)
* المصفوفة ثنائية الأبعاد (m x n): يكون حجم المدخلات بعدد عناصر المصفوفة (n x m)
* المصفوفة الأحادية (1 x n): يكون حجم المدخلات بعدد عناصر المصفوفة (n)
* الرقم الواحد: لا نعتبر حجم المدخلات ١ عند حساب كفاءة الخوارزمية، وإنما يتم حسابه بعدد البت في التمثيل الثنائي، باستخدام اللوغارتمات، على سبيل المثال لو كان العدد المدخل هو ١٦ فإن حجم المدخل هو ٤ لأن (log2[16] = 4). وسنرى لاحقا تأثير هذا الافتراض في حساب كفاءة الخوارزميات
قياس وقت التنفيذ للخوارزمية
في تحليل كفاءة الخوارزميات لا يمكن الاعتماد على قياس وقت التنفيذ الفعلي للخوارزمية والذي يقاس بالثانية وأجزائها. والسبب في ذلك أن هذا الوقت يعتمد على عوامل خارجية لا علاقة لها بتصميم الخوارزمية
في تحليل كفاءة الخوارزميات لا يمكن الاعتماد على قياس وقت التنفيذ الفعلي للخوارزمية والذي يقاس بالثانية وأجزائها. والسبب في ذلك أن هذا الوقت يعتمد على عوامل خارجية لا علاقة لها بتصميم الخوارزمية
ومن هذه العوامل سرعة الحاسب المستخدم، وطريقة كتابة البرنامج الذي ينفذ الخوارزمية، ولغة البرمجة المستخدمة، والمترجم المستخدم في إنشاء كود الآلة، إضافة إلى صعوبة تسجيل وقت التنفيذ الفعلي للبرنامج نظرا لوجود برامج أخرى تستخدم نفس الموارد المتاحة من المعالج والذاكرة.
في تحليل الخوارزميات يتم قياس وقت التنفيذ من خلال تحديد أهم عملية في الخوارزمية، تسمى العملية الأساسية أو المهيمنة، وهي العملية التي لها المساهمة الأكبر في إجمالي وقت التشغيل، ومن ثم يتم حساب عدد المرات التي يتم فيها تنفيذ العملية الأساسية. وسوف أوضح هذه الفكرة باستخدام مثالين.
مثال ١: خوارزمية إيجاد العدد الأصغر في مصفوفة مكونة من (n) من العناصر. تحتوي هذه الخوارزمية على ٣ عمليات:
* عملية إسناد في السطر ١ تنفذ مرة واحدة
* عملية مقارنة في السطر ٣ تنفذ في كل دورة من حلقة التكرار
* عملية إسناد في السطر ٤ تنفذ في كل مرة يتحقق الشرط في المقارنة
* عملية إسناد في السطر ١ تنفذ مرة واحدة
* عملية مقارنة في السطر ٣ تنفذ في كل دورة من حلقة التكرار
* عملية إسناد في السطر ٤ تنفذ في كل مرة يتحقق الشرط في المقارنة
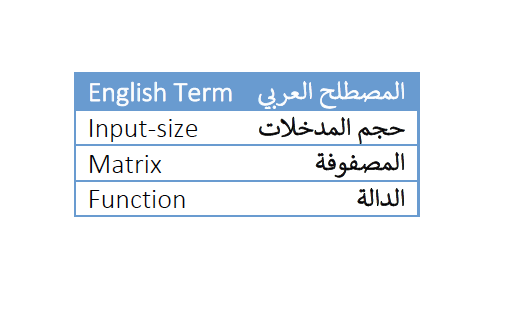
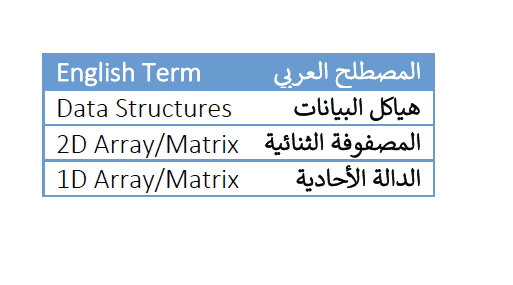
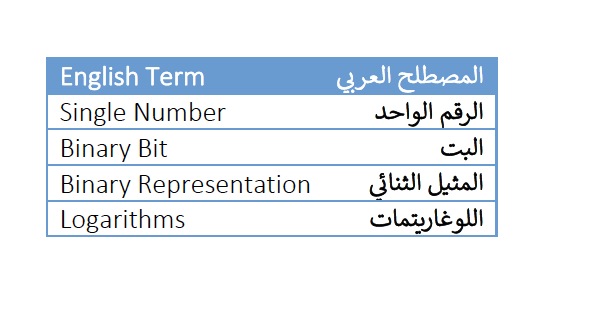
إذا العملية الأساسية في هذه الخوارزمية هي عملية المقارنة ويتم تكرارها (n-1) من المرات لأن حلقة التكرار يتم تنفيذها من (2) إلى (n). وبالتالي يمكن تعريف وقت التنفيذ للخوارزمية كدالة في حجم المدخلات على النحو التالي:
T(n) = n - 1
T(n) = n - 1
ملاحظة: هذه الخوارزمية تحتاج وحدة ذاكرة واحدة لتخزين المتغير (minval)، وبالتالي يمكن حساب كفاءة المساحة كدالة في حجم المدخلات على النحو التالي:
S(n)=1
S(n)=1
مثال ٢: خوارزمية حساب عدد البت في التمثيل الثنائي لعدد صحيح موجب. على سبيل المثال عدد البت في التمثيل الثنائي للعدد ٥ (101) هو ٣ بت.
تحتوي الخوارزمية على ٤ عمليات:
* إسناد في السطر ١ تنفذ مرة ١
* مقارنة في السطر ٢ تنفذ في كل دورة من حلقة التكرار عند تحقق الشرط ومرة عندما لا يتحقق الشرط
* إسناد في السطر ٣ تنفذ في كل مرة يتحقق الشرط في حلقة التكرار
* قسمة في السطر ٤ تنفذ في كل مرة يتحقق الشرط في حلقة التكرار
* إسناد في السطر ١ تنفذ مرة ١
* مقارنة في السطر ٢ تنفذ في كل دورة من حلقة التكرار عند تحقق الشرط ومرة عندما لا يتحقق الشرط
* إسناد في السطر ٣ تنفذ في كل مرة يتحقق الشرط في حلقة التكرار
* قسمة في السطر ٤ تنفذ في كل مرة يتحقق الشرط في حلقة التكرار
العملية الأساسية في هذه الخوارزمية هي عملية المقارنة ويتم تكرارها (log(n)+1) لأن قيمة (n) تتناقص بمقدار النصف في كل مرة حتى تصبح قيمتها صفر إضافة إلى مرة أخيرة عندما لا يتحقق الشرط.
ولتوضيح ذلك نأخذ الرقم ١٥ كمثال، حيث تبدأ الخوارزمية بالعدد ١٥ ثم يتناقص بمقدار النصف في كل مرة (١٥، ٧، ٣، ١، ٠)، وعددها ٤ (log(15)+1=3+1=4) وبالتالي يمكن تعريف وقت التنفيذ للخوارزمية على النحو التالي:
T(n)=⌊log(n)⌋+1
T(n)=⌊log(n)⌋+1
وهنا يجب التنبيه على أننا اتفقنا على تمثيل وقت تنفيذ الخوارزمية كدالة في حجم المدخلات (أي حجم العدد المدخل)، وعلى الرغم من أن الحساب السابق صحيح إلا أنه لا يوضح كفاءة الخوارزمية لأنه تم قياسه باستخدام قيمة العدد المدخل وليس بحجم المدخلات.
وحيث أن حجم العدد المدخل يقاس بعدد البت (m) في التمثيل الثنائي لهذا العدد، والذي يمكن حسابه باستخدام دالة اللوغارتمات الثنائية ( [m=log2[n ). وبناء عليه يمكن إعادة كتابة تعريف وقت التنفيذ كدالة بحجم العدد المدخل على النحو التالي
T(m)=m+1
أي المعادلتين تمثل خوارزمية كفاءتها أفضل؟
T(m)=m+1
أي المعادلتين تمثل خوارزمية كفاءتها أفضل؟
معدلات النمو:
عند تحليل كفاءة الخوارزميات نهتم بمعدل تزايد وقت تنفيذ الخوارزمية كلما زاد حجم المدخلات، وهو ما يسمى معدل النمو. وتوضح الصورة معدلات النمو لعدد من الدوال المختلفة.
عند تحليل كفاءة الخوارزميات نهتم بمعدل تزايد وقت تنفيذ الخوارزمية كلما زاد حجم المدخلات، وهو ما يسمى معدل النمو. وتوضح الصورة معدلات النمو لعدد من الدوال المختلفة.
وهذه المعدلات تتأثر بما يسمى الحد المهيمن الموجود في معادلة حساب وقت التنفيذ، وبالتالي يمكن تجاهل الحدود غير المؤثرة والقيم الثابتة عند حساب معدل النمو. على سبيل المثال يمكن تبسيط المعادلة التالية بحذف الحدود ذات الأس الأدنى وكذلك المعاملات والقيم الثابتة.
وتجدر الإشارة إلى أنه يمكن تقسيم الخوارزميات من حيث معدل النمو إلى نوعين رئيسيين:
النوع الأول: الخوارزميات ذات الوقت متعدد الحدود وهي خوارزميات يكون الحد الأعلى لمعدل نموها عبارة عن دالة متعددة الحدود، وهذا النوع من الخوارزميات يمكن تنفيذه بشكل عملي لحل المشكلة بوقت معقول.
النوع الأول: الخوارزميات ذات الوقت متعدد الحدود وهي خوارزميات يكون الحد الأعلى لمعدل نموها عبارة عن دالة متعددة الحدود، وهذا النوع من الخوارزميات يمكن تنفيذه بشكل عملي لحل المشكلة بوقت معقول.
النوع الثاني: الخوارزميات ذات الوقت الأسي وهي خوارزميات يكون الحد الأعلى لمعدل نمو وقت تنفيذها عبارة عن دالة أسية، وهذا النوع من الخوارزميات لا يمكن تنفيذه بشكل عملي لحل المشكلة في وقت معقول، ويتم الاستعاضة عن هذه الخوارزميات بحلول تقريبية للحصول على حلول قريبة من الحل الأمثل.
جاري تحميل الاقتراحات...