(١)
يشيع استخدام الرياضيات في دراسة الفيزياء. ومع استشعار بعض الطلاب لأهميتها، إلا أن البعض الآخر يتساءل عن فائدتها. حتى كبار الفيزيائيين تساءلوا ولكن بطريقة مختلفة! تساءلوا عن الفائدة الهائلة للرياضيات في الفيزياء. في هذه السلسلة نعرض أشهر هذه التساؤلات وهو للفيزيائي يوجين ويجنر
يشيع استخدام الرياضيات في دراسة الفيزياء. ومع استشعار بعض الطلاب لأهميتها، إلا أن البعض الآخر يتساءل عن فائدتها. حتى كبار الفيزيائيين تساءلوا ولكن بطريقة مختلفة! تساءلوا عن الفائدة الهائلة للرياضيات في الفيزياء. في هذه السلسلة نعرض أشهر هذه التساؤلات وهو للفيزيائي يوجين ويجنر
(٢)
إن مما يثير الدهشة أن بعض الأفكار الرياضية قد تُستخدم في دراسة بعض الظواهر التي لا يمكن أن نتصور أي ترابط بينها!
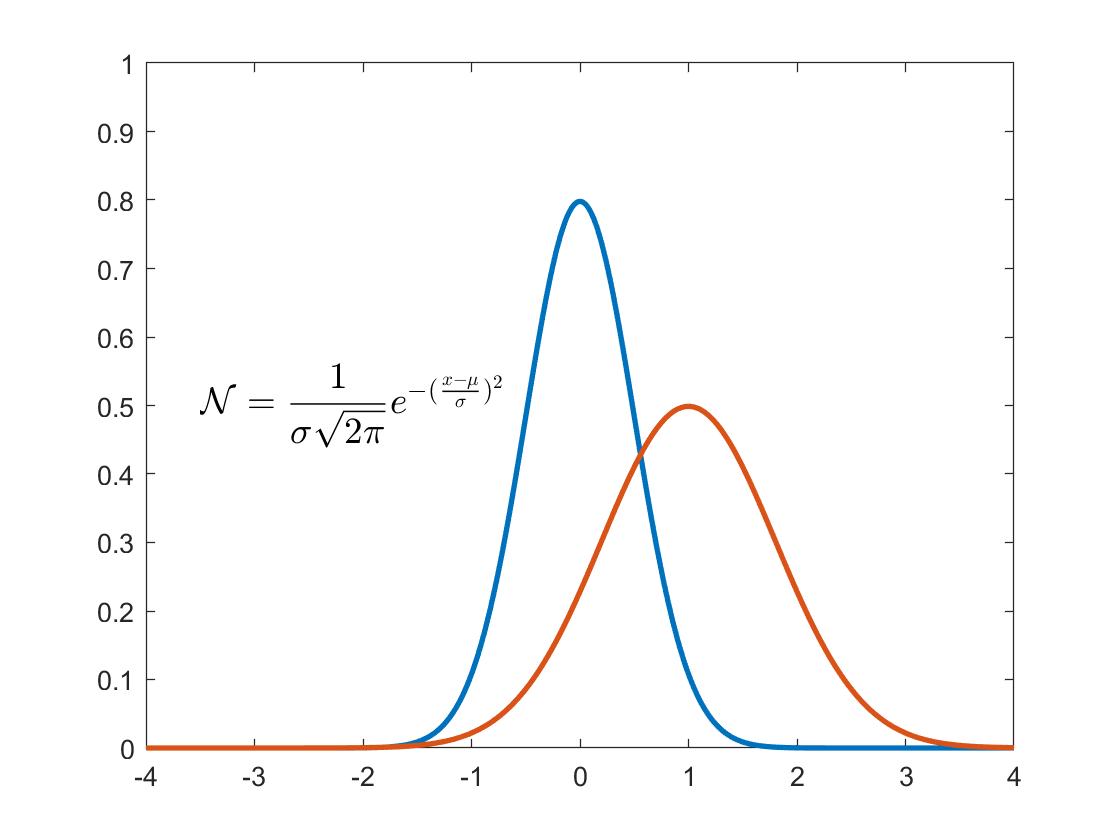
من الأمثلة التي قد تدهشنا عند التأمل فيها هو توزيع جاوس الإحصائي —و يعد أهم توزيع إحصائي— ويستخدم لوصف الكثير من الظواهر مثل توزيع أطوال البشر وضغط الدم وغيرها.
إن مما يثير الدهشة أن بعض الأفكار الرياضية قد تُستخدم في دراسة بعض الظواهر التي لا يمكن أن نتصور أي ترابط بينها!
من الأمثلة التي قد تدهشنا عند التأمل فيها هو توزيع جاوس الإحصائي —و يعد أهم توزيع إحصائي— ويستخدم لوصف الكثير من الظواهر مثل توزيع أطوال البشر وضغط الدم وغيرها.
(٣)
لو ألقينا نظرة على معادلة هذا التوزيع، سنرى أنها تحتوي على الرقم باي "π". ولو سألَنا البعض عن ماهيَة الرقم باي، لقُلنا أنه نسبة محيط أي دائرة إلى قطرها. كيف لعدد مرتبط بالدائرة أن يكون له استخدامات لوصف التوزيع الإحصائي لضغط الدم عند البشر؟!
لو ألقينا نظرة على معادلة هذا التوزيع، سنرى أنها تحتوي على الرقم باي "π". ولو سألَنا البعض عن ماهيَة الرقم باي، لقُلنا أنه نسبة محيط أي دائرة إلى قطرها. كيف لعدد مرتبط بالدائرة أن يكون له استخدامات لوصف التوزيع الإحصائي لضغط الدم عند البشر؟!
(٤)
وحديثًا ظهر استعمال المفاهيم الرياضية الطوبولوجية في الفيزياء. فقد نشأت الأفكار الطوبولجية بهدف تصنيف الأشكال الهندسية -التي قد تبدو مختلفة- إلى فئات تجمعها بعض العوامل المشتركة. كمثال: نعتبر الكُوب وحلوى الدونات متكافئين طوبولجيًّا، والسبب هو امتلاكهما لنفس العدد من الفجوات
وحديثًا ظهر استعمال المفاهيم الرياضية الطوبولوجية في الفيزياء. فقد نشأت الأفكار الطوبولجية بهدف تصنيف الأشكال الهندسية -التي قد تبدو مختلفة- إلى فئات تجمعها بعض العوامل المشتركة. كمثال: نعتبر الكُوب وحلوى الدونات متكافئين طوبولجيًّا، والسبب هو امتلاكهما لنفس العدد من الفجوات
(٥)
فحاليًّا تعد مفاهيم الطوبولوجيا من أهم الطرق النظرية المتقدمة في الفيزياء لتصنيف
حالات المواد الكمّية Quantum Phases of Matter.
فتحت هذه المفاهيم الرياضية مجالاً جديداً وواسعاً اسمه "حالات المادة الطوبولوجية" والذي أدى إلى فوز ثلاثه من رواده بجائزة نوبل عام 2016
فحاليًّا تعد مفاهيم الطوبولوجيا من أهم الطرق النظرية المتقدمة في الفيزياء لتصنيف
حالات المواد الكمّية Quantum Phases of Matter.
فتحت هذه المفاهيم الرياضية مجالاً جديداً وواسعاً اسمه "حالات المادة الطوبولوجية" والذي أدى إلى فوز ثلاثه من رواده بجائزة نوبل عام 2016
(٦)
وفقًا لوِيجنر، فإن بعض المفاهيم الرياضية تبدو منطقية فقد تم اقتراحها بفضل تجربتنا الحياتية. ولكن بعض المفاهيم الأخرى (مثل الأعداد المركبة) يصعب تصور أنها تكونت بسبب تجربتنا. على الرغم من هذا، فلها تأثير كبير في الكثير من النظريات الأخرى مثل نظرية المعادلات والدوال التحليلية.
وفقًا لوِيجنر، فإن بعض المفاهيم الرياضية تبدو منطقية فقد تم اقتراحها بفضل تجربتنا الحياتية. ولكن بعض المفاهيم الأخرى (مثل الأعداد المركبة) يصعب تصور أنها تكونت بسبب تجربتنا. على الرغم من هذا، فلها تأثير كبير في الكثير من النظريات الأخرى مثل نظرية المعادلات والدوال التحليلية.
(٧)
النوع الآخر من المفاهيم الرياضية تطور فقط بسبب فُضول علماء الرياضيات! مهاراتهم في التلاعب بالكميات والمفاهيم الرياضية التي لديهم أدّى إلى التوصل لمفاهيم أخرى جديدة. يقول ويجنر إن جمال الرياضيات الجديدة هي دليل على فن وبراعة العالم الرياضيّ الذي توصل لها.
النوع الآخر من المفاهيم الرياضية تطور فقط بسبب فُضول علماء الرياضيات! مهاراتهم في التلاعب بالكميات والمفاهيم الرياضية التي لديهم أدّى إلى التوصل لمفاهيم أخرى جديدة. يقول ويجنر إن جمال الرياضيات الجديدة هي دليل على فن وبراعة العالم الرياضيّ الذي توصل لها.
(٨)
أما بالنسبة للفيزياء، فإن ويجنر يقول أن تطورها كعلم يدرس الطبيعة كان سيستحيل لولا خاصيتان للظواهر الطبيعية التي يهمنا دراستها وهما:
1/ عدم تغير الظواهر بتغير الزمان أو المكان (اللاتغير "Invariance")
2/ تأثر الظواهر الفيزيائية بعدد قليل جدا من المتغيرات الخارجية (Irrelevancy)
أما بالنسبة للفيزياء، فإن ويجنر يقول أن تطورها كعلم يدرس الطبيعة كان سيستحيل لولا خاصيتان للظواهر الطبيعية التي يهمنا دراستها وهما:
1/ عدم تغير الظواهر بتغير الزمان أو المكان (اللاتغير "Invariance")
2/ تأثر الظواهر الفيزيائية بعدد قليل جدا من المتغيرات الخارجية (Irrelevancy)
(٩)
فلو كانت الظواهر الطبيعية في الرياض تختلف عنها في جدة أو كانت تختلف اليوم عن الغد، لما كان هناك ظواهر متكررة حتى نسعى لتفسيرها؛ فهي تتغير في كل مكان وزمان. ولو كان عدد المتغيرات الخارجية المؤثرة على الظواهر كبيراً جداً لما استطعنا دراستها.
فلو كانت الظواهر الطبيعية في الرياض تختلف عنها في جدة أو كانت تختلف اليوم عن الغد، لما كان هناك ظواهر متكررة حتى نسعى لتفسيرها؛ فهي تتغير في كل مكان وزمان. ولو كان عدد المتغيرات الخارجية المؤثرة على الظواهر كبيراً جداً لما استطعنا دراستها.
(١٠)
ولابد أيضا من التنبيه إلى أن قوانين الطبيعة (كما نَصيغها) هي عبارة عن جمل شرطية، ولا تضمن لنا تحقق الشرط في الأصل. فإن تحقق الشرط تحققت النتيجة وأحيانا – كما في فيزياء الكم – تحقق الشرط يؤدي إلى احتمال تحقق النتيجة.
ولابد أيضا من التنبيه إلى أن قوانين الطبيعة (كما نَصيغها) هي عبارة عن جمل شرطية، ولا تضمن لنا تحقق الشرط في الأصل. فإن تحقق الشرط تحققت النتيجة وأحيانا – كما في فيزياء الكم – تحقق الشرط يؤدي إلى احتمال تحقق النتيجة.
(١١)
بعد أن تحدّث ويجنر عن أهم خصائص الرياضيات والفيزياء، يخبرنا الآن عن دور الرياضيات. فيقول أن لها دورين في الفيزياء. الأول روتينيّ وهو استخدامها للقيام بالحسابات والحصول على نتائج رقمية من نظريات موجودة ومعروفة. أما الثاني –وهو الأهم– فهو دورها في صياغة النظريات الفيزيائية.
بعد أن تحدّث ويجنر عن أهم خصائص الرياضيات والفيزياء، يخبرنا الآن عن دور الرياضيات. فيقول أن لها دورين في الفيزياء. الأول روتينيّ وهو استخدامها للقيام بالحسابات والحصول على نتائج رقمية من نظريات موجودة ومعروفة. أما الثاني –وهو الأهم– فهو دورها في صياغة النظريات الفيزيائية.
(١٢)
عادةً تمر عملية صنع النظريات الفيزيائية بخطوتين.
أولا: وجود نموذج تصوّري فيزيائي لما يحدث. وثانيا: تحويل النموذج الفيزيائي إلى نموذج رياضي.
قد يكون النموذج التصوّري ناتجًا عن ملاحظتنا المباشرة للطبيعة، أو نابعًا من فهمنا لنموذج رياضي سابق هو في الأصل ناتج عن نموذج تصوّري آخر
عادةً تمر عملية صنع النظريات الفيزيائية بخطوتين.
أولا: وجود نموذج تصوّري فيزيائي لما يحدث. وثانيا: تحويل النموذج الفيزيائي إلى نموذج رياضي.
قد يكون النموذج التصوّري ناتجًا عن ملاحظتنا المباشرة للطبيعة، أو نابعًا من فهمنا لنموذج رياضي سابق هو في الأصل ناتج عن نموذج تصوّري آخر
(١٣)
نستطيع تقسيم النظريات الفيزيائية إلى ثلاث فئات.
أولًا: نظريات يلعب فيها النموذج التصوري الدور الأساسي، ولا يأتي النموذج الرياضي بما لا يمكن تخيله وفقا للنموذج التصوري (تكون المخرجات في مستوى المدخلات).
قوانين نيوتن للحركة ونظريته للجاذبية مثال على ذلك.
نستطيع تقسيم النظريات الفيزيائية إلى ثلاث فئات.
أولًا: نظريات يلعب فيها النموذج التصوري الدور الأساسي، ولا يأتي النموذج الرياضي بما لا يمكن تخيله وفقا للنموذج التصوري (تكون المخرجات في مستوى المدخلات).
قوانين نيوتن للحركة ونظريته للجاذبية مثال على ذلك.
(١٤)
ثانيًا: نظريات تُبنى على نموذج تصوري ولكن النموذج الرياضي يأتي بمفاجآت لا يمكن توقعها (المخرجات أكثر من المدخلات).
ومثالها هو النظرية الموجية للضوء الناتجة عن النظرية الكهرومغناطيسية، وأيضا صياغة ميكانيكا الكم القائمة على المصفوفات والناتجة عن النظرية القديمة لذرة الهيدروجين
ثانيًا: نظريات تُبنى على نموذج تصوري ولكن النموذج الرياضي يأتي بمفاجآت لا يمكن توقعها (المخرجات أكثر من المدخلات).
ومثالها هو النظرية الموجية للضوء الناتجة عن النظرية الكهرومغناطيسية، وأيضا صياغة ميكانيكا الكم القائمة على المصفوفات والناتجة عن النظرية القديمة لذرة الهيدروجين
(١٥)
ثالثًا وهو النوع الأغرب: نظريات لا يسبقها نموذج تصوري، فهي فقط نماذج رياضية! (مخرجات بدون مدخلات) لا تدخل فيها الفيزياء التجريبية إلا في مرحلة التأكد من توقعاتها. نعم هنالك نظريات كثيرة من هذا النوع ونظرية انزياح لامب "Lamb shift" مثال على ذلك.
ثالثًا وهو النوع الأغرب: نظريات لا يسبقها نموذج تصوري، فهي فقط نماذج رياضية! (مخرجات بدون مدخلات) لا تدخل فيها الفيزياء التجريبية إلا في مرحلة التأكد من توقعاتها. نعم هنالك نظريات كثيرة من هذا النوع ونظرية انزياح لامب "Lamb shift" مثال على ذلك.
(١٦)
لو حُق لنا وشبهنا النظريات الفيزيائية، فهي كالأحلام! بعض الأحلام لها علاقة بما عِشته في يومك وبعضها لا صلة لها بما صادفته طيلة حياتك. إن تحقق الثاني كان هذا أكثر ما قد يصيبك بالدهشة في حياتك. النوع الثاني من الأحلام يشبه النوع الثالث من النظريات.
لو حُق لنا وشبهنا النظريات الفيزيائية، فهي كالأحلام! بعض الأحلام لها علاقة بما عِشته في يومك وبعضها لا صلة لها بما صادفته طيلة حياتك. إن تحقق الثاني كان هذا أكثر ما قد يصيبك بالدهشة في حياتك. النوع الثاني من الأحلام يشبه النوع الثالث من النظريات.
(١٧)
إنّ النوعين الثاني والثالث من النظريات هما سبب تعجب ويجنر –وغيره من العلماء– من دور الرياضيات في الفيزياء.
التعجب هذا يقودنا إلى شيء أكثر إثارة، يقودنا إلى تساؤلات أكبر، يقودنا إلى الحيرة!
إنّ النوعين الثاني والثالث من النظريات هما سبب تعجب ويجنر –وغيره من العلماء– من دور الرياضيات في الفيزياء.
التعجب هذا يقودنا إلى شيء أكثر إثارة، يقودنا إلى تساؤلات أكبر، يقودنا إلى الحيرة!
(١٨)
وبما أن الفيزيائين بشكل عام يثقون في نظرياتهم بتحقق شيئين:
توافق توقعات النظرية مع النتائج التجريبية، وعدم تعارضها مع بعض القواعد الأساسية في الفيزياء (مثل الحد الأعلى للسرعة، عدم كسر التناظرات، وغيرها...)،
وبما أن الفيزيائين بشكل عام يثقون في نظرياتهم بتحقق شيئين:
توافق توقعات النظرية مع النتائج التجريبية، وعدم تعارضها مع بعض القواعد الأساسية في الفيزياء (مثل الحد الأعلى للسرعة، عدم كسر التناظرات، وغيرها...)،
(١٩)
فإن مجرد التوافق بين العمل النظري والتجريبي ليس دليلا على الصحة المطلقة للنظرية. فبعض النظريات –رغم نجاحها الكبير– إلا أننا ندرك جيدًا أنها نظريات في أصلها قاصرة ومحدودة التطبيق وبالتالي لابد من البحث عن بديل (مثل نموذج الإلكترونات الحرة والمستخدم لفهم عدد من خصائص الموصلات)
فإن مجرد التوافق بين العمل النظري والتجريبي ليس دليلا على الصحة المطلقة للنظرية. فبعض النظريات –رغم نجاحها الكبير– إلا أننا ندرك جيدًا أنها نظريات في أصلها قاصرة ومحدودة التطبيق وبالتالي لابد من البحث عن بديل (مثل نموذج الإلكترونات الحرة والمستخدم لفهم عدد من خصائص الموصلات)
(٢٠)
وبما أننا لا نستطيع الجزم بالصحة المطلقة يأتي سؤال آخر: هل نظرياتنا الحالية صحيحة؟ وإن كانت كذلك، فهل هي فريدة؟ ألا يمكن صياغة نظريات أخرى لا يتشابه ظاهرها مع النظريات الحالية، ولكنها تستطيع وصف الطبيعة بنفس الدقة، وربما أفضل؟
سنترك لكم هذه التساؤلات، ونختم هنا :)
-انتهى-
وبما أننا لا نستطيع الجزم بالصحة المطلقة يأتي سؤال آخر: هل نظرياتنا الحالية صحيحة؟ وإن كانت كذلك، فهل هي فريدة؟ ألا يمكن صياغة نظريات أخرى لا يتشابه ظاهرها مع النظريات الحالية، ولكنها تستطيع وصف الطبيعة بنفس الدقة، وربما أفضل؟
سنترك لكم هذه التساؤلات، ونختم هنا :)
-انتهى-
جاري تحميل الاقتراحات...